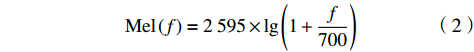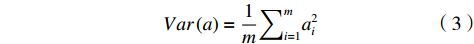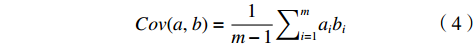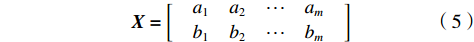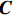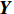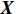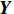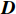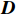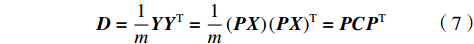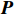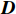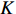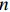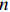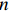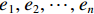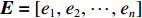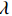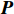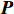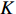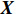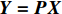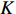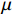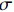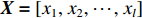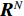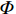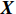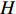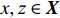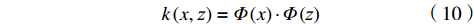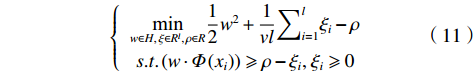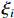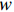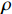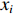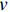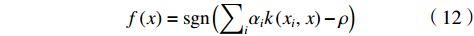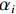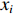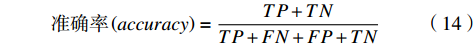Machine tool fault classification and diagnosis based on sound fusion feature and OCSVM
-
摘要: 针对数控机床工作中诊断维护困难的问题,提出一种利用声音融合特征搭配一类支持向量机(OCSVM)的故障诊断和SVM故障分类的方法。首先采集不同工作状态下的数控机床运行音频数据,采用梅尔频率倒谱系数(MFCC)和线性预测倒谱系数(LPCC)方法对数据进行多维特征提取,通过PCA降维归一化后融合特征,最后将处理好的特征进行OCSVM检测是否存在故障,并且识别故障类别。研究采集了数控机床正常工作和9类异常故障音作为数据集开展分析。通过实验证明,基于声音特征融合与OCSVM可以实现对数控机床故障的准确诊断,诊断准确率能达到96.1%,通过SVM能对数控机床故障精准分类,分类准确率能达到93.3%。Abstract: Aiming at the problem of difficult diagnosis and maintenance in CNC machine work, a method of fault diagnosis and SVM fault classification using sound fusion features and one class support vector machine (OCSVM) is proposed. Firstly, the audio data of CNC machine operation under different working conditions are collected. The Mel frequency Cepstral coefficient (MFCC) and linear prediction Cepstral coefficient (LPCC) methods are used to extract multi-dimensional features of the data. After dimension reduction and normalization by PCA, the features are fused. Finally, the processed features are detected by OCSVM to determine whether there is a fault and identify the fault category. The normal operation of the CNC machine and nine types of abnormal fault tones are collected as data sets for analysis. Experiments show that the sound feature fusion and OCSVM can realize the accurate diagnosis of CNC machine faults, and the diagnosis accuracy can reach 96.1%. The CNC machine faults can be accurately classified by SVM, and the classification accuracy can reach 93.3%.
-
Keywords:
- OCSVM /
- abnormal sound detection /
- feature fusion /
- dimension reduction /
- fault diagnosis
-
高档数控机床和基础制造装备是实现制造技术和工业现代化的基石[1],也是实施强国战略的重点领域,全球制造业强国也都在研究水平先进的制造设备。由于数控机床结构复杂,零部件构造精密,在运行时很容易被周围各种因素影响,加上长时间不停歇的使用,导致设备故障频繁发生[2],对产品性能和数控机床寿命都会产生影响,如果在问题刚出现或即将出现时能快速反馈并采取解决措施,就能挽回更多损失,因此精准的故障分类诊断就成了生产过程的重要环节。机械故障诊断技术通过采集和分析设备运行时的数据,可以了解和掌握机器在运行过程中的状态,实现对设备运行状态的监测。常采用的诊断技术包括油液监测、振动监测、性能趋势分析和无损探伤等,其中早期最常用的是基于接触式振动传感器的诊断方法,该方法在齿轮、高压断路器等故障部位的应用较为成熟,但该方法需要接触测量,将振动传感器放置在被测物体上,当遇到高温、腐蚀液体、难以附着的光滑位置等问题时,该方法无法发挥作用;此外,振动传感器也只能对机械的局部问题进行故障检测,当局部的振动特征对故障不敏感时,诊断效率会受到影响。随着声音技术的发展,基于声音的故障诊断技术逐渐受到更多研究人员的关注,该技术采用非接触式测量,无需将传感器附着在被测机械位置上,可以将机械整体声音进行收集处理,操作简单且灵活。近年来声学故障检测也逐渐得到推广,应用在多种机械领域上,如钻机钻头的断裂检测[3]、刨机故障诊断[4]等。
常见的特征提取方法有时频域分析[5]、小波变换[6]等,但单一的特征提取方法往往不能充分表征数控机床音频信息,因此使用Mel频率倒谱系数(mel-frequency cepstral coefficient,MFCC)提取特征和线性预测倒谱系数(linear predictive cepstral coefficient,LPCC)提取特征融合,从不同标准获得更多数控机床声音特征;因为特征的维度较高,数据处理较慢,使用主成分分析(PCA)降维方法和归一化处理特征数据,可以消除不同维度和量纲导致的距离计算不合理情况;传统的诊断方法只有在正常和异常样本均衡时才会有较高的检测准确率,而数控机床工作时的异常样本(如刀具断裂、主轴磨损等)难以大量获取,因此使用一类支持向量机方法对数控机床数据进行检测可以解决样本不均衡的问题。本文将利用MFCC和LPCC方法提取数控机床声音信号的多维特征,分别进行PCA降维和归一化后进行特征融合,将融合特征使用一类支持向量机方法判断是否存在故障,若检测为正常,则继续工作,若判断为异常,则通过SVM分类器[7]识别具体故障类别并停止工作,精准定位故障快速解决问题。通过该流程能快速且高效诊断识别数控机床的故障类别。
1. 算法原理
1.1 LPCC特征提取
在声音特征参数提取技术的发展历程中,线性预测倒谱系数最早被用于语音特征参数的提取,该方法能较好反映语音的声道特征。随着环境音的发展,虽然工程机械音与语音产生过程有所差异,但通过对比分析语音与机械环境音的产生和特征,在本质上发音过程类似,且常规的部分特征都适用,因此,可使用LPCC对机械音进行特征分析[8]。
LPCC是由线性预测编码 (linear predicative coding,LPC)计算频谱包络得到的倒谱系数,因为LPC对误差比较敏感,导致一些小误差也会造成频谱质量下降。LPCC具有计算量小,对共振峰的描述清晰等优点,其核心思想是:第
$ n $ 个音频样本可以通过其之前$ p $ 个样本的线性组合来估计,表示为$$ s\left(n\right)\approx {a}_{1}s(n-1)+\cdots +{a}_{p}s(n-p) $$ (1) 式中:
$ {a}_{1},{a}_{2},\cdots ,{a}_{p} $ 被假定为语音分析框架上的常数[9]。LPCC特征的阶数通常与其所反映的信息和运算量成正比,阶数越大,通常所包含的信息就越大,阶数通常选择8~16[10]。特征提取声谱图如图1所示,这是对声音信号进行预加重、分帧和加窗等预处理后,再进行线性预测分析、快速傅里叶变化、取对数和快速傅里叶逆变化获得的关键特征信息。1.2 MFCC特征提取
不同于LPCC对发声处机理进行研究而得到的声学特征,MFCC是依据人耳的听觉系统研究推出的特征提取方法。与LPCC类似的是,MFCC也是利用求倒谱系数分析特征,倒谱分析是常用的一种方法,它可以用有限特征表征声音包含的信息。
这种方法不基于信号本质的变化,对输入的声音信号不附加各种条件,又利用了听觉模型上的研究,因此这种特征提取方法具有更强的鲁棒性[11],而且在信噪比较低时仍有可观的检测正确率。通过将频率转换成Mel尺度,特征能够更好地匹配人类的听觉感知效果,从频率到Mel频率的转换公式为
$$ \mathrm{M}\mathrm{e}\mathrm{l}\left(f\right)=2\;595\times {{\rm{lg}}}\left(1+\frac{f}{700}\right) $$ (2) 其中:f为频率,利用Mel滤波也是该特征提取方法的一个关键,MFCC的特征提取声谱图如图2所示,图2中MFCC的特征声谱图是经过对声音信号预处理、快速傅里叶变化、Mel滤波、取对数以及离散余弦变化后获得的关键特征信息。
1.3 PCA特征降维
通常特征的维度越高,其所包含的信息就越多,准确率也会相应提高,但当处理的文件数量增多,且特征维度较高时,一次检测运行可能就是以小时起步,因此为了节省时间与内存,选择一种合适的降维算法进行处理数据就显得格外重要。不同的算法会根据数据的不同特性进行降维,常见的降维方法有t分布随机邻域嵌入(t-SNE[12])、一致流形近似与投影(UMAP)和PCA方法。
PCA是主成分分析方法。这是一种常见的数据处理算法,一般用来给高维数据降维。通过选择不同的基对同一组数据给出不同的表示,若基的数量小于数据本身的维数,则说明达到了降维的目标[13]。其中的关键问题是怎样选择
$ K $ 个基去表示$ N $ 维向量。(1)方差。方差代表着数值的分散程度,为方便处理,将变量均值化为0可得
$$ Var\left(a\right)=\frac{1}{m}{\sum }_{i=1}^{m}{a}_{i}^{2} $$ (3) 需要寻找1个一维基,使得变换数据到基上后,方差值最大。
(2)协方差。协方差能代表1个变量之间的相关性。要让2个变量之间不存在线性相关性,这样能使其表示更多不重复的原始信息。同样将均值化为0可得
$$ {{Cov}}(a,b)=\frac{1}{m-1}{\sum }_{i=1}^{m}{a}_{i}{b}_{i} $$ (4) 当协方差为0时,表示2个变量线性不相关,在选择第2个基时在第1个基正交的方向上进行选择,就能满足相互正交的期望。
(3)协方差矩阵。要满足优化目标,就要将方差与协方差统一表示,可用矩阵的方式,假设有a和b两个变量,按行组成矩阵
$ \boldsymbol{X} $ $$ \boldsymbol{X}=\left[\begin{array}{c}\begin{array}{cccc}{a}_{1}& {a}_{2}& \cdots & {a}_{m}\end{array}\\ \begin{array}{cccc}{b}_{1}& {b}_{2}& \cdots & {b}_{m}\end{array}\end{array}\right] $$ (5) 然后求
$ \boldsymbol{X} $ 的协方差矩阵$ \boldsymbol{C} $ $$ \boldsymbol{C}=\frac{1}{m}\boldsymbol{X}{\boldsymbol{X}}^{\mathrm{T}}=\left[\begin{array}{cc}{{Cov}}(a,a)& {{Cov}}(a,b)\\ {{Cov}}(b,a)& {{Cov}}(b,b)\end{array}\right] $$ (6) 由式(6)可得统一表达后的方差与协方差。
(4)矩阵对角化。假设
$ \boldsymbol{P} $ 是1组基按行组成的矩阵,设$ \boldsymbol{Y}=\boldsymbol{P}\boldsymbol{X} $ ,则$ \boldsymbol{Y} $ 就是$ \boldsymbol{X} $ 对$ \boldsymbol{P} $ 做基变换后的数据。设$ \boldsymbol{Y} $ 的协方差矩阵为$ \boldsymbol{D} $ ,则$ \boldsymbol{D} $ 为$$ \boldsymbol{D}=\frac{1}{{m}}\boldsymbol{Y}{\boldsymbol{Y}}^{\mathrm{T}}=\frac{1}{{m}}\left(\boldsymbol{P}\boldsymbol{X}\right)(\boldsymbol{P}\boldsymbol{X}{)}^{\mathrm{T}}=\boldsymbol{P}\boldsymbol{C}{\boldsymbol{P}}^{\mathrm{T}} $$ (7) 由式(7)可以看出优化目标已经变为寻找1个矩阵
$ \boldsymbol{P} $ ,满足$ \boldsymbol{D} $ 是1个对角矩阵,则对角元素从大到小的前$ K $ 行就是要寻找的基。由实对称矩阵定义可知,1个
$ n $ 行$ n $ 列实对称矩阵一定能找到$ n $ 个单位正交特征向量,设为$ {e}_{1},{e}_{2},\cdots ,{e}_{n} $ ,将其按列组成矩阵$ \boldsymbol{E}=\left[{e}_{1},{e}_{2},\cdots ,{e}_{n}\right] $ ,则协方差矩阵$ \boldsymbol{C} $ 可为$$ {\boldsymbol{E}}^{\mathrm{T}}\boldsymbol{C}\boldsymbol{E}={\boldsymbol{\varLambda}} =\left[\begin{array}{cccc}{\lambda }_{1}& & & \\ & {\lambda }_{2}& & \\ & & \ddots & \\ & & & {\lambda }_{N}\end{array}\right] $$ (8) 对角元素
$ \lambda $ 就是各特征向量对应的特征值。得到$ \boldsymbol{P}={\boldsymbol{E}}^{\mathrm{T}} $ ,$ \boldsymbol{P} $ 的每1行都是$ \boldsymbol{C} $ 的1个特征向量,将$ \boldsymbol{P} $ 从大到小排列的前$ K $ 行组成的矩阵乘原始数据$ \boldsymbol{X} $ ,就得到了$ \boldsymbol{Y}=\boldsymbol{P}\boldsymbol{X} $ ,即为降到$ K $ 维后的数据。文章对比了t-SNE、UMAP以及PCA 这3种降维方法诊断效果,具体实验见后文。
1.4 特征融合
传统理解中,特征维度越高代表其所包含的关键信息越多,检测准确率就会相应地提高。环境声具有非线性且背景复杂发声点较多,使得单一特征无法完全表征环境声音信号,融合特征可以解决这一问题。因此,采用LPCC与MFCC方法提取特征,之后进行降维及归一化处理,最后结合生成新的特征。
$$ {{\boldsymbol{X}}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{d}}=\frac{{{\boldsymbol{X}}}_{i}-\mu }{\sigma } $$ (9) 其中:
$ \mu $ 为所有样本数据的均值,$ \sigma $ 为所有样本数据的标准差。如式(9),对数据进行标准归一化,是机器学习与统计学习任务中常用的一种处理方式。由于MFCC和LPCC是基于不同方法的滤波器提取得到的特征,具有不同的量纲,因此直接对两者进行叠加或结合可能会导致精度下降。为了消除量纲不同带来的影响,采用特征降维和标准归一化处理可以解决由于不同维度和量纲导致的距离计算不合理情况,此外还能方便处理数据和加快收敛速度。
文章对两种特征提取方法都设置为13维特征提取,因此MFCC和LPCC特征具有相同的维数,在经过降维、归一化处理后,声谱图已转换为多维数组,利用Python中的concatenate函数将处理后的2种特征的对应位置相互融合,融合后的新特征既包含MFCC提取的特征信息,也包含LPCC提取的特征信息,2种方法提取的特征之间相关性较小,反映出环境声音不同特征,预计融合后效果较好。
1.5 OCSVM分类法
一类支持向量机(one-class support vector machine,OCSVM)是由Bernhard Scholkopf等人基于支持向量机(SVM)提出[14]。SVM有着诸多算法不具备的优良特性,首先,SVM算法是基于统计学习中VC维与结构风险最小原理的典型机器学习方法。通过添加对应的正则项,使该方法具有良好的泛化能力,不易过拟合;将SVM的原二次规划求解问题转化为凸优化问题,当数据集线性可分时,则必定能得到全局最优解;其次利用线性、多项式和高斯等核函数,将原样本空间投影至高维空间,利用高维空间线性可分的特性,将非线性问题转化为线性问题进行求解;最后,通过引用一个松弛变量和惩罚系数,最大化软分类间隔,使得SVM算法具有较好的鲁棒性。
OCSVM算法也使用了核函数来处理线性不可分的情况。给定数据
$ \boldsymbol{X}=\left[{x}_{1},{x}_{2},\cdots ,{x}_{l}\right] $ ,其中包含l个观测数量,设为1个${\boldsymbol{R}}^{{N}}$ 的1个子集,假设$ \varPhi $ 是1个从$ \boldsymbol{X} $ 低维输入空间到高维Hilbert空间$ H $ 的映射,利用核函数运算通过k(x, z)对任意$ x,{\textit{z}}\in \boldsymbol{X} $ :$$ k\left(x,{\textit{z}}\right)=\varPhi \left(x\right)\cdot \varPhi \left({\textit{z}}\right) $$ (10) 为了将数据集与原点分离,并使这个距离最大化,对其求解二次规划,得
$$ \left\{\begin{array}{c}\underset{w\in {H}\text{,}\xi \in {R}^{l},\rho \in R}{\text{min}}\dfrac{1}{2}{‖w‖}^{2}+\dfrac{1}{vl}{\displaystyle\sum }_{i=1}^{l}{\xi }_{i}-\rho \\ s.t.\left(w\cdot \varPhi \left({x}_{i}\right)\right)\geqslant \rho -{\xi }_{i},{\xi }_{i}\geqslant 0\end{array}\right. $$ (11) 由于非零松弛变量
$ {\xi }_{i} $ 在目标函数中受到惩罚,可以预期,如果$ w $ 和$ \rho $ 解决了这个问题,则对于训练集中包含的大多数示例$ {x}_{i} $ ,决策函数将会为正,其中$ v $ 扮演重要权衡角色,$ v\in \left(\mathrm{0,1}\right) $ 是1个参数,类似于SVM中的惩罚参数$ C $ 。采用拉格朗日求解,并通过上面核函数可证明解具有SV展开式:$$ f\left(x\right)={{\rm{sgn}}}\left({\sum }_{i}{\alpha }_{i}k\left({x}_{i},x\right)-\rho \right) $$ (12) 具有非零
$ {\alpha }_{i} $ 的模式$ {x}_{i} $ 称为SVs,其中找到系数便可得优化问题的对偶形式:$$ \left\{\begin{array}{c}\underset{\alpha }{\text{min}}\dfrac{1}{2}{\displaystyle\sum }_{i,j}{\alpha }_{i}{\alpha }_{j}k({x}_{i},{x}_{j})\\ s.t.0\leqslant {\alpha }_{i}\leqslant \dfrac{1}{vl},{\displaystyle\sum }_{i}{\alpha }_{i}=1\end{array}\right. $$ (13) 单分类支持向量机基本思想:首先通过非线性变换将数据映射到高维的特征空间,然后在特征空间中,将原点作为异常点,求出训练样本与原点的最大间隔的超平面。对测试样本,通过超平面进行分类[15]。这是一种无监督学习方法,能规避手工贴标错误引起的识别下降,还能节省大量时间。为预防将通过的人声鸟叫等都识别为异常声音,所以在训练测试时,会给定一个总比例约0.1的异常样本,使机器认识异常样本,通过机器自动识别异常样本数量,对比已知数据观察检测效果。
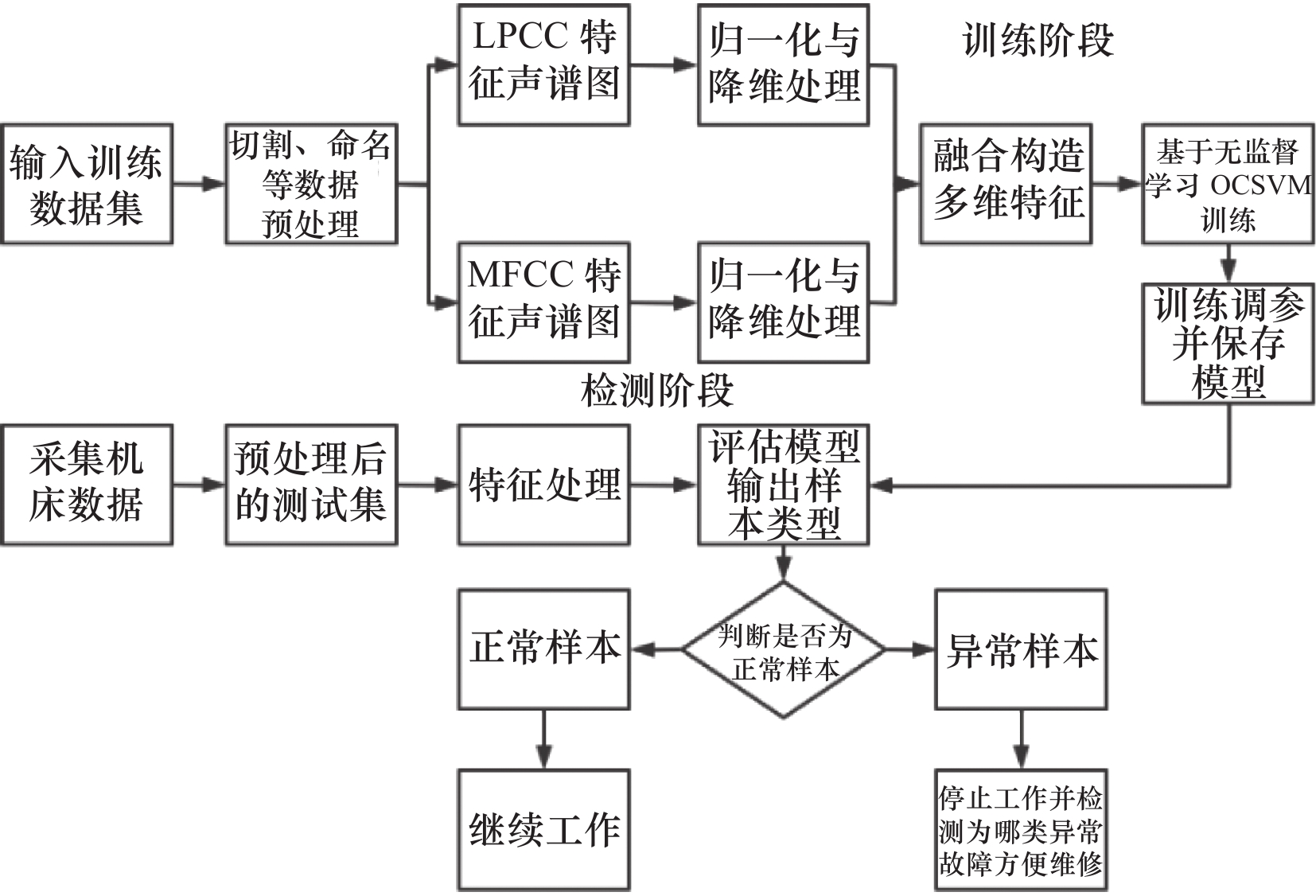
2. 基于声音特征融合与OCSVM的机床故障分类诊断方法
机床的异音故障分类诊断方案主要有以下3个方面的工作,分别是机床音频信号的采集、数据信号的处理和异音诊断方法的实现。根据实现的流程,将机床异音检测系统分为以下几步:
(1)使用Brüel & Kjær(BK)信号采集设备(包括传声器、信号采集仪等)采集机床正常工作与多种异常工作的声音信号,为后续算法分析提供数据支持。
(2)对采集的信号先在BK Pulse Reflex软件上进行时频域观察分析,再通过Python进行切割命名等处理数据,使用MFCC和LPCC方法进行信号滤波和特征提取,选择PCA降维方法进一步处理特征,对提取的两种特征进行特征融合,为之后的决策方法处理好数据。
(3)利用OCSVM方法对机床音频数据进行检测,得到是否有异常音频,若为异常音频,再进一步判断是哪一类异常音频。
基于声音特征融合与OCSVM的机床故障分类诊断详细流程图如图3所示。
3. 实验研究
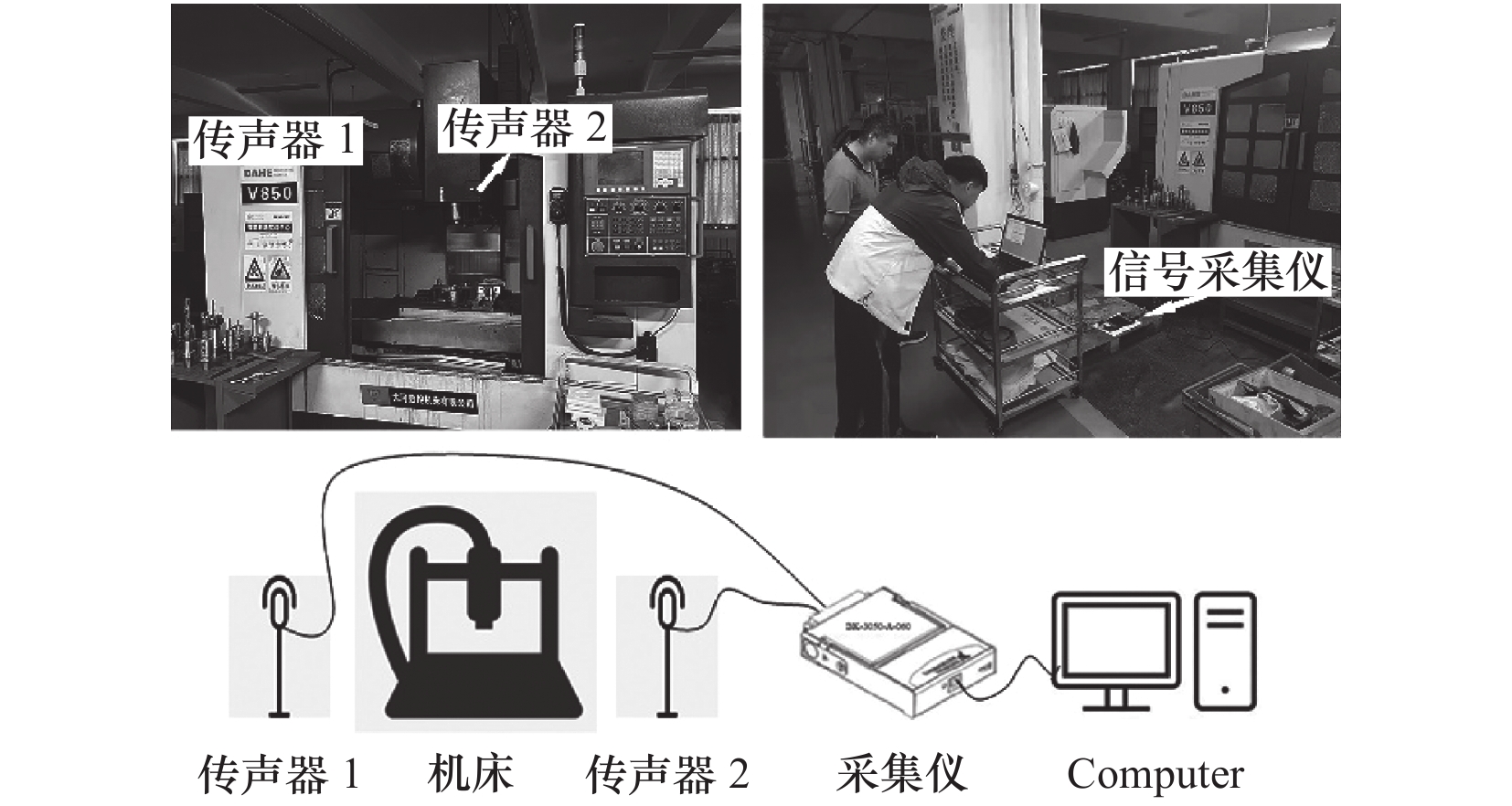
实验采用Type 4189-A-021传声器和Type0671前置放大器采集数控机床的各类音频,搭配3050-A-060信号采集仪传入计算机进行数据分析,传声器悬挂放置在机床内部两侧,传声器方法采集数据区别于振动传感器,不能放置在机床的某一单独位置附近,应确保对工作环境的整体监测,同时对传声器包裹海绵套,在滤除部分杂音和降噪的同时保护设备正常使用,部分设置参考GB/T 12060.4声系统设备第4部分:传声器测量方法,测试图如图4所示。
机床音频信号数据采集时,先确定正常运转的各项参数值,选择8 mm尺寸的切削刀具,机床转速设置为3 000 r/min,进给量为250 mm/min,背吃刀量为1 mm。刀具磨损音频采集选择70%左右界值的磨损刀具进行工作,进给量增至350 mm/min时运行状态作为异常音频采集,背吃刀量增至1.5 mm时作为异常音频采集。考虑到不同的异常音频故障采集难度不同,因此每个音频的采集数量都会有区别,如刀具断裂录制时间较短,采用音频裁剪的方式扩充数据集。采集频率为51.2 kHz,使用双声道采集音频,数据每30 s分为一个音频文件,后期切割为每500 ms一个音频文件,并去除其中的空白音频,录制的各类正常与异常音频总数如表1所示。
表 1 实验采集数据信息数据类别 样本数量/个 数据类别 样本数量/个 正常运行 3 182 刀具磨损 547 刀具缺失 600 主轴抱死 473 刀具断裂 65 导轨磨损 70 刀具空转 600 进给量 600 异常撞击 568 背吃刀量 600 机床数据采集过程中会存在环境噪声的影响,采用2种方法解决该问题:第一种是在声音特征提取时对信号预处理、加滤波器滤除部分噪音;第二种是对持续存在的机床噪音混入每一个音频中,将采集的机床每类音频都设为一个整体,默认该噪声为数据集的一部分去训练诊断。
对机床的所有类型音频信号进行时频谱分析如图5所示,从左上图至由右下图分别为刀具磨损、刀具断裂、刀具缺失、主轴抱死、导轨磨损、进给量改变、背吃刀量改变、异常撞击、刀具空转和正常工作时频图。由图5对比可见,刀具断裂和导轨磨损的异常音频与机床正常运转的声音差别较大,其他7种异音时频图与正常声音时频图差别会小很多,因此可以选择更多的分析方式识别故障。
分别使用MFCC和LPCC各提取机床音频信号特征进行实验检测,在异音故障检测上主要设置特征融合和降维方法的选择对比实验。理论上融合特征会获得更高的检测效果,因此先固定融合特征选择效果更好的降维方法,待确定降维方法后,再进行单特征与多特征提取实验对比。实验中以9∶1比例选择正常与异常样本,由于本文采用的诊断方法是OCSVM,可以在数据样本不均衡的情况下使用,选择训练数据样本总量为2 828个,测试样本总量为701个,将所有异常故障声音合并为一个整体称为故障总类,具体每一类的训练和测试数据量如表2所示。
表 2 训练/测试样本数量说明数据类别 样本数量/个 数据类别 样本数量/个 正常运行 2 545/637 刀具磨损 34/8 刀具缺失 35/8 主轴抱死 35/6 刀具断裂 35/7 导轨磨损 10/6 刀具空转 29/8 进给量 35/7 异常撞击 35/7 背吃刀量 35/7 数据样本量为n为2 828,数据时长为500 ms,每一次检测模型会对数据特征处理,将每一个数据点的值表示出来,计算得到结果,如表3所示。
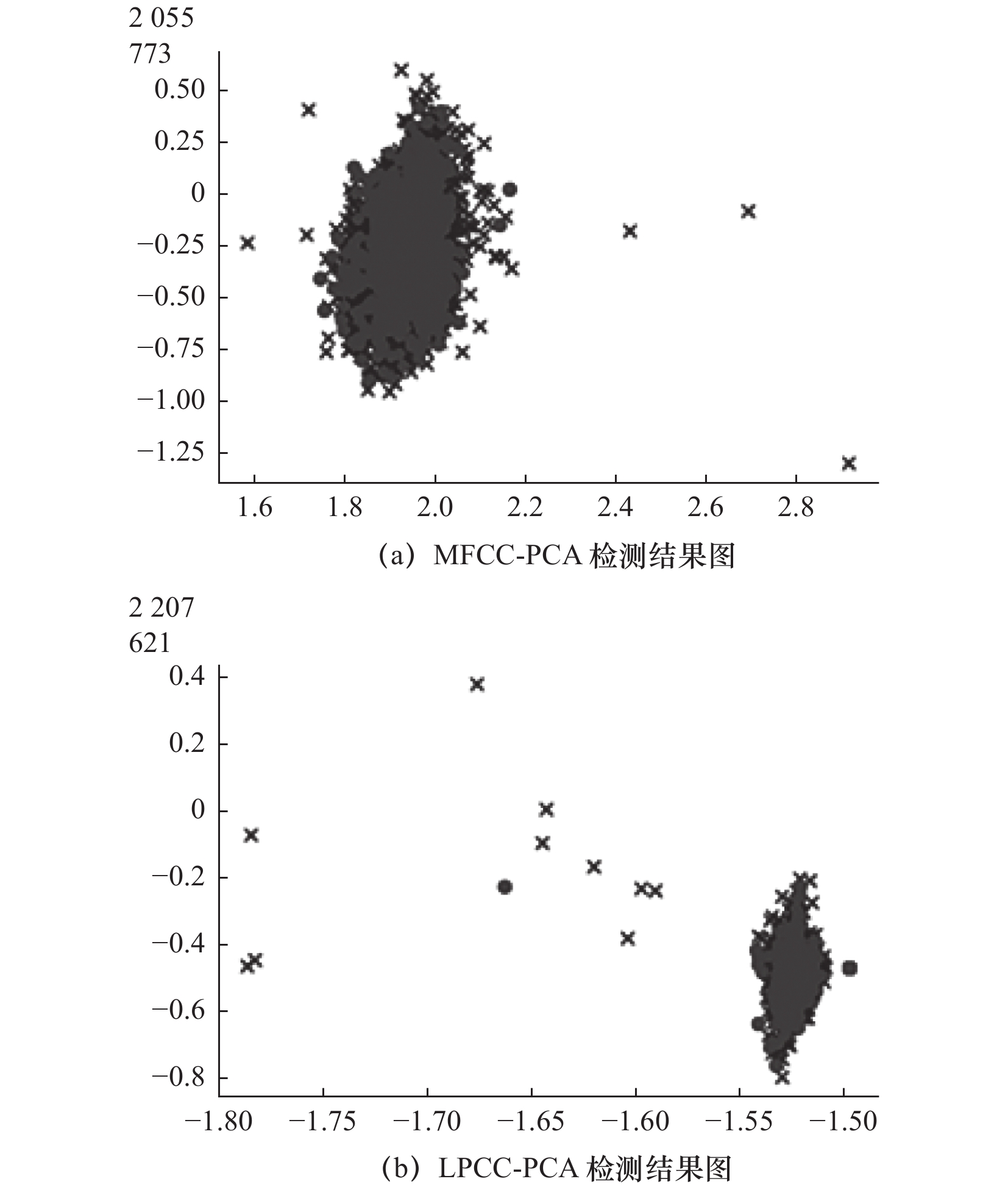
表 3 单次检测数据值表示1 2 … 499 500 1 1.917 961 3 0.175 864 2 0.248 575 3 0.635 663 2 2 1.940 552 3 −0.560 507 6 0.515 331 6 0.546 546 6 … … n 1.947 884 7 −0.504 686 8 0.471 540 3 0.190 711 2 分别对机床音频数据进行t-SNE、UMAP和PCA 降维方法实验,并进行调参,实验结果如图6。
在保持核函数和多特征融合方法情况下,常用混淆矩阵表达模型数据预测结果,见表4。
表 4 混淆矩阵预测值 真实值 正例 假例 正例 真正例$ TP $ 伪假例$ FN $ 假例 伪正例$ FP $ 真假例$ TN $ 采用式(14)准确率方法来体现模型效果。
$$ \mathrm{准}\mathrm{确}\mathrm{率}\left(accuracy\right)=\frac{TP+TN}{TP+FN+FP+TN} $$ (14) 通过准确率对比特征融合下不同降维方法的检测效果,如表5所示。
表 5 3种降维方法检测结果对比融合特征-降维 训练样本 正确识别 运行时间/s 准确率 t-SNE 2 828 2 543 1 632 0.899 UMAP 2 828 2 685 5 322 0.949 PCA 2 828 2 683 188 0.949 t-SNE降维方法在2 828个数据中共识别错285个,这种效果并不尽如人意。UMAP降维方法在2 828个数据中识别错143个,识别准确率相比t-SNE较高,但识别时间增加过多。PCA方法在所选的数据中识别率较高,且运行时间较短,说明PCA降维方法相对更加合适。
在确定PCA降维方法后,开始进行单特征提取与多特征融合的实验,对机床音频数据集进行单独MFCC和LPCC特征提取实验,并进行调参,结果如图7所示,详细信息如表6所示。
表 6 单特征检测结果单特征-PCA 训练样本 正确识别 运行时间/s 准确率 MFCC-PCA 2 828 2 338 83 0.827 LPCC-PCA 2 828 2 490 86 0.881 由图7和表6可见单特征效果较好的为LPCC特征提取,检测效果为88.1%,在运行时间差距不大的情况下,检测效果相比于表5中特征融合-PCA方法的94.9%准确率还是低了6.8%,因此特征融合和PCA降维方法搭配OCSVM分类器使用是诊断故障效果最好的方法,下面将使用该方法进行测试验证。
将测试数据代入训练好的故障诊断模型,诊断效果如图8所示。
由图8检测效果可见正确诊断样本674个,错误诊断样本27个,故障诊断准确率达到了96.1%,能够实现机床运行故障的诊断。
通过机床异音故障诊断后,当诊断为正常工作声音时,机床正常工作,当诊断为异常声音时,需要进一步识别该音频对应的机床故障类别并停止机器,通过K近邻(K-nearest neighbors,KNN)方法和SVM方法进行具体检测。机床异音故障分类的总数为4 123个样本,共9类如表7所示。
表 7 机床异音故障类别样本数量数据类别 样本数量/个 数据类别 样本数量/个 刀具磨损 547 刀具断裂 65 刀具缺失 600 主轴抱死 473 刀具空转 600 导轨磨损 70 进给量 600 背吃刀量 600 异常撞击 568 将整体数据以7∶3分为训练集与测试集进行实验,观察测试集检测效果,实验结果如表8所示。
表 8 多类故障检测结果对比检测方法 分类样本总数 正确识别 运行时间/s 准确率 KNN 1 237 977 160 0.790 SVM 1 237 1 154 153 0.933 由表8可见SVM检测效果相比KNN方法准确率提高了14.3%,因此在检测异音故障问题上选择SVM方法能更准确地检测出异音所属故障类别。通过机床故障分类的检测方法流程,可以对大多数故障问题进行分类诊断,大大降低因故障带来的各项损失。
4. 结语
文章提出一种基于声音特征融合与OCSVM的异音故障分类诊断方法,并将该方法应用于机床实际工作,进行了故障诊断与分类,由实验结果得到以下结论:
(1)将LPCC与MFCC提取的特征进行融合可以获得机床声音数据更完整的各项信息,故障诊断准确率分别比MFCC和LPCC高12.2%和6.8%,说明对数据进行特征融合会获得更好的诊断效果。
(2)对比t-SNE、UMAP和PCA降维方法,通过机床故障诊断实验结果可见,无论是故障诊断准确率还是诊断时间,PCA都属于效果更好的方法,因此使用PCA对机床数据进行降维处理。
(3)通过机床测试数据集的故障诊断实验可见,即使在样本不均衡的情况下,OCSVM分类器的故障诊断准确率也能达到96.1%,说明该方法契合此类异常样本难以获取的应用方向且环境噪音对诊断的结果影响不大。由多类故障检测结果说明了在机床故障分类诊断应用上,SVM是比KNN更好的分类方法。
-
表 1 实验采集数据信息
数据类别 样本数量/个 数据类别 样本数量/个 正常运行 3 182 刀具磨损 547 刀具缺失 600 主轴抱死 473 刀具断裂 65 导轨磨损 70 刀具空转 600 进给量 600 异常撞击 568 背吃刀量 600 表 2 训练/测试样本数量说明
数据类别 样本数量/个 数据类别 样本数量/个 正常运行 2 545/637 刀具磨损 34/8 刀具缺失 35/8 主轴抱死 35/6 刀具断裂 35/7 导轨磨损 10/6 刀具空转 29/8 进给量 35/7 异常撞击 35/7 背吃刀量 35/7 表 3 单次检测数据值表示
1 2 … 499 500 1 1.917 961 3 0.175 864 2 0.248 575 3 0.635 663 2 2 1.940 552 3 −0.560 507 6 0.515 331 6 0.546 546 6 … … n 1.947 884 7 −0.504 686 8 0.471 540 3 0.190 711 2 表 4 混淆矩阵
预测值 真实值 正例 假例 正例 真正例$ TP $ 伪假例$ FN $ 假例 伪正例$ FP $ 真假例$ TN $ 表 5 3种降维方法检测结果对比
融合特征-降维 训练样本 正确识别 运行时间/s 准确率 t-SNE 2 828 2 543 1 632 0.899 UMAP 2 828 2 685 5 322 0.949 PCA 2 828 2 683 188 0.949 表 6 单特征检测结果
单特征-PCA 训练样本 正确识别 运行时间/s 准确率 MFCC-PCA 2 828 2 338 83 0.827 LPCC-PCA 2 828 2 490 86 0.881 表 7 机床异音故障类别样本数量
数据类别 样本数量/个 数据类别 样本数量/个 刀具磨损 547 刀具断裂 65 刀具缺失 600 主轴抱死 473 刀具空转 600 导轨磨损 70 进给量 600 背吃刀量 600 异常撞击 568 表 8 多类故障检测结果对比
检测方法 分类样本总数 正确识别 运行时间/s 准确率 KNN 1 237 977 160 0.790 SVM 1 237 1 154 153 0.933 -
[1] 张迎新, 刘翔宇. 基于专利共类的高端机床制造核心技术关联特征识别−以五轴联动数控机床为例[J]. 情报杂志, 2018, 37(2): 50-56. DOI: 10.3969/j.issn.1002-1965.201707386 [2] 王建榕. 数控机床的故障检测与维修探析[J]. 中国设备工程, 2021(17): 160-161. DOI: 10.3969/j.issn.1671-0711.2021.17.099 [3] Tran T, Lundgren J. Drill fault diagnosis based on the scalogram and mel spectrogram of sound signals using artificial intelligence[J]. IEEE Access, 2020, 8: 203655-203666. DOI: 10.1109/ACCESS.2020.3036769
[4] Cui P, Wang J J, Li X B, et al. Sub-health identification of reciprocating machinery based on sound feature and OOD detection[J]. Machines, 2021, 9(8): 179-179. DOI: 10.3390/machines9080179
[5] 彭博, 张毅, 蹇清平, 等. 快速路径的多时频曲线时变转速轴承故障诊断[J]. 制造技术与机床, 2020(9): 148-154. DOI: 10.19287/j.cnki.1005-2402.2020.09.030 [6] Kuo J Y, You S Y, Lin H C, et al. Constructing condition monitoring model of wind turbine blades[J]. Mathematics, 2022, 10(6): 972-972. DOI: 10.3390/math10060972
[7] 牛博雅, 杨斌, 孙杰. 面向生产现场的刀具磨损状态监测研究[J]. 制造技术与机床, 2020(11): 104-109. DOI: 10.19287/j.cnki.1005-2402.2020.11.022 [8] 杨三伟. 基于OSALPCC与SVM的工程机械声音识别算法研究[D]. 杭州: 杭州电子科技大学, 2016. [9] Wang T L, Cao J W, Pei L Y. A novel underground pipeline surveillance system based on hybrid acoustic features[J]. IEEE Sensors Journal, 2021, 21(2): 1040-1050. DOI: 10.1109/JSEN.2020.3009112
[10] 史水平, 李世作. 线性预测编码(LPC)技术及其在音频文件上的应用[J]. 现代电子技术, 2004(4): 21-23. DOI: 10.3969/j.issn.1004-373X.2004.04.007 [11] 张进, 吴健, 欧习洋, 等. 基于特征降维和神经网络的电能表内异物声音自动识别[J]. 机械设计与制造, 2021(3): 234-237. DOI: 10.3969/j.issn.1001-3997.2021.03.053 [12] Kobak D, Linderman G C. Initialization is critical for preserving global data structure in both t-SNE and UMAP[J]. Nature Biotechnology, 2021, 39(2): 156-157.
[13] 符垚慧梅, 徐强, 陈学振. 基于PCA特征提取和驱动电流的数控机床进给轴状态检测[J]. 制造技术与机床, 2021(2): 32-35. DOI: 10.19287/j.cnki.1005-2402.2021.02.005 [14] Olkopf B S, Williamson R, Smola A, et al. Support vector method for novelty detection[C]. Advances in Neural Information Processing Systems, 2000: 582–588.
[15] 牟少敏, 时爱菊. 模式识别与机器学习技术[M]. 北京: 冶金工业出版社, 2019: 62-63. -
期刊类型引用(2)
1. 令晓明,陈鸿雁,张小玉,张真. 基于ASP-SERes2Net的说话人识别算法. 北京工业大学学报. 2025(01): 42-50 .  百度学术
百度学术
2. 张新文,周苗苗,李金辉. 基于谱图小波阈值的机床主轴振动数字信号降噪研究. 制造技术与机床. 2023(10): 164-168+183 .  本站查看
本站查看
其他类型引用(3)




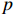
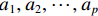

 下载:
下载: