Research on coordinated motion trajectory planning method of dual robots with different constraints
-
摘要: 随着工业机器人在各行各业的广泛使用,单个机器人已不能满足大规模工件的搬运、复杂焊接和孔轴组装等要求。在双机器人的研究中,最重要的问题就是如何保证双机器人间的运动满足时间和空间约束,也就是双机器人的多重运动协调。文章用两台机械臂协同搬运和协同写字的实例分别分析了紧约束和松约束下的协同运动,对其运动学协调关系进行分析,通过工件或主体运动轨迹研究机器人约束关系,构建两双机协同体系;在Matlab中进行稳定性验证,并对所提出的理论进行可靠性验证。Abstract: With the widespread use of industrial robots in all walks of life, a single robot can no longer meet the requirements of large-scale workpiece handling, complex welding, and hole shaft assembly. In the research of dual robots, the most important problem is how to ensure that the motion between the two robots meets the time and space constraints, that is, the coordination of multiple movements of the two robots. In this paper, the cooperative motion under tight and loose constraints is analyzed by using the examples of cooperative handling and collaborative writing of two robotic arms, and the kinematic coordination relationship is analyzed, and the robot constraint relationship is studied through the workpiece or main body motion trajectory to construct a two-machine collaborative system. Stability verification is carried out in Matlab, and the proposed theory is verified for reliability.
-
Keywords:
- dual-robot /
- coordinated movement /
- trajectory planning
-
在工业自动化程度不断提高的今天,在复杂的生产环境下,单机器人难以满足现实的需求,如大型搬运、孔轴部件的装配、复杂表面的焊接等。与单机器人相比,双机器人不仅要考虑工作空间和外部约束,还要考虑二者的运动协调关系,它们在进行配合作业时就建立了约束关系。
Saridis G N[1]提出了面向复杂环境的高层决策模式,这种模式以智能与精度为核心,将系统划分为3个层次,最低控制是低智能、高精度的,最高控制是高智能、低精度的。Kasagami F等[2]提出了双机协同焊接的控制方法,两个机器人分别夹持工件和进行焊接,对夹持工件的机器人示教,焊接机器人根据运动学约束自动寻找并跟踪焊接位置。该方法避免了多次示教引起误差,缩短了准备时间。李洋等[3]构建了基于RRT的双机协作平台,并对其进行了轨迹规划。王雷[4]通过集中控制系统,使两台机器人在时间和空间上保持一致,并提出了两种解决方案:点对点规划和路径规划。孟石等[5]在Ke-Scope平台上,对两个机器人的叠加和耦合运动模式进行了分析,并对两个机器人的协同工作进行了程序设计和仿真。
本文以JLRB8-600 型机器人为研究对象,以协调搬运和协调写字为例,分别研究紧约束和松约束运动,分析其运动学关系及空间约束关系,使用 Matlab进行实验验证。
1. 机器人运动学建模
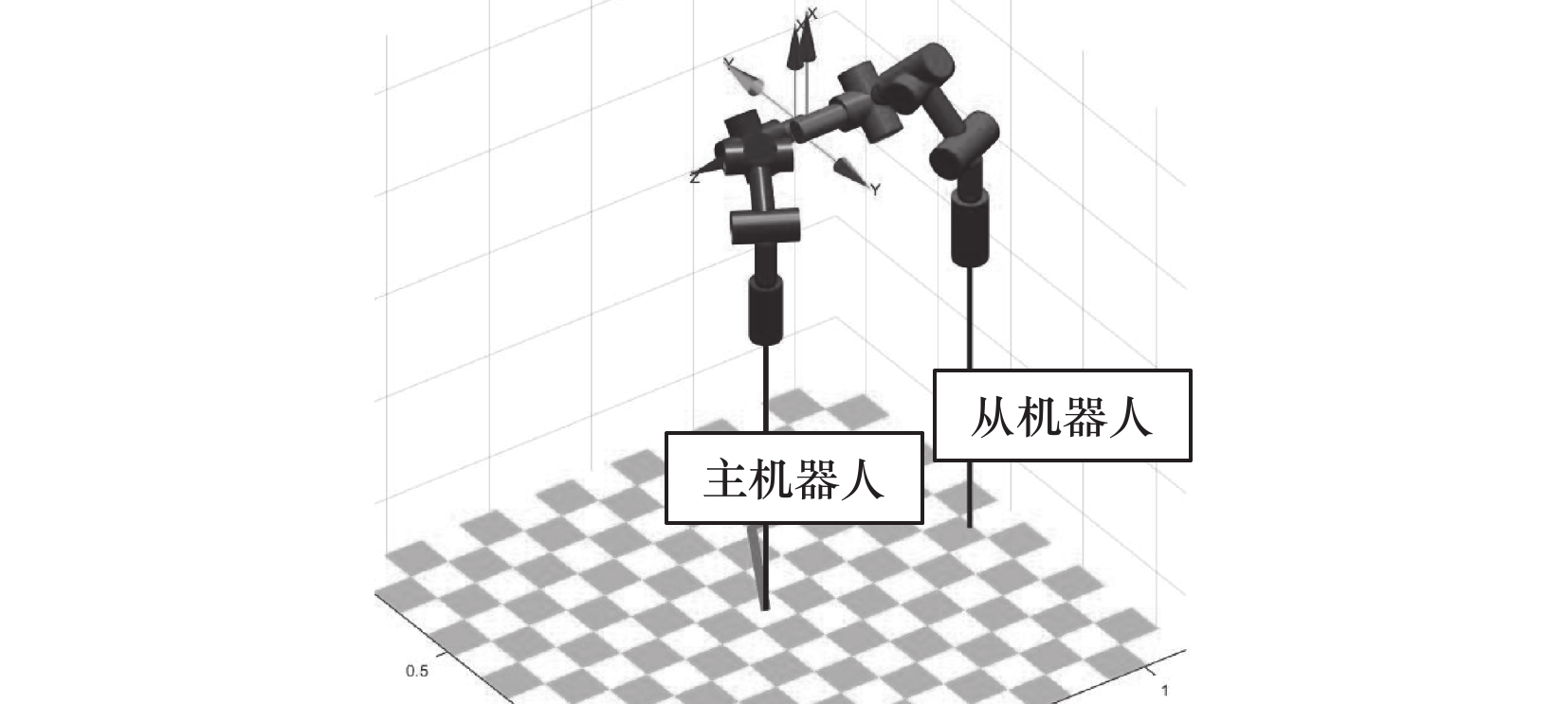
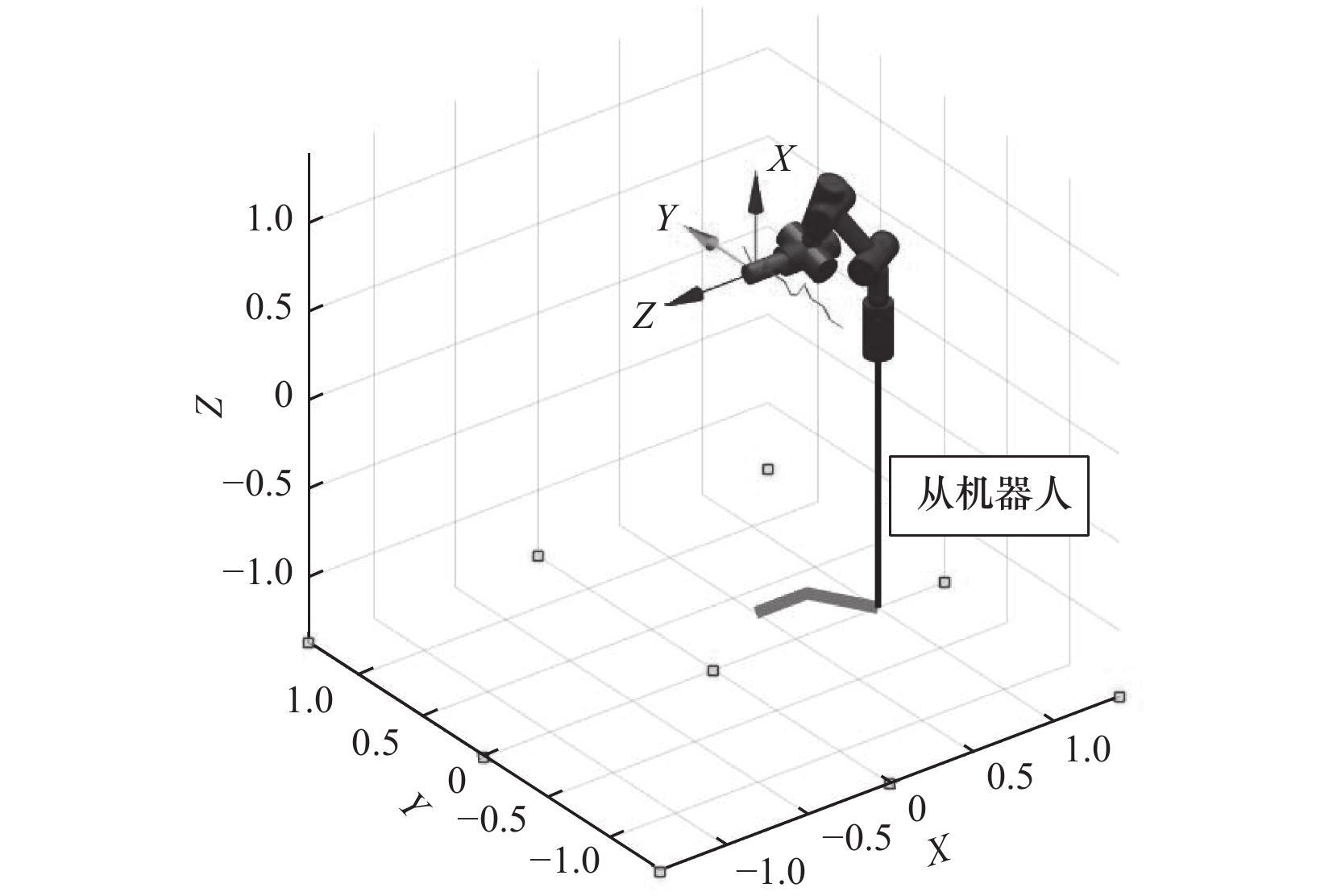
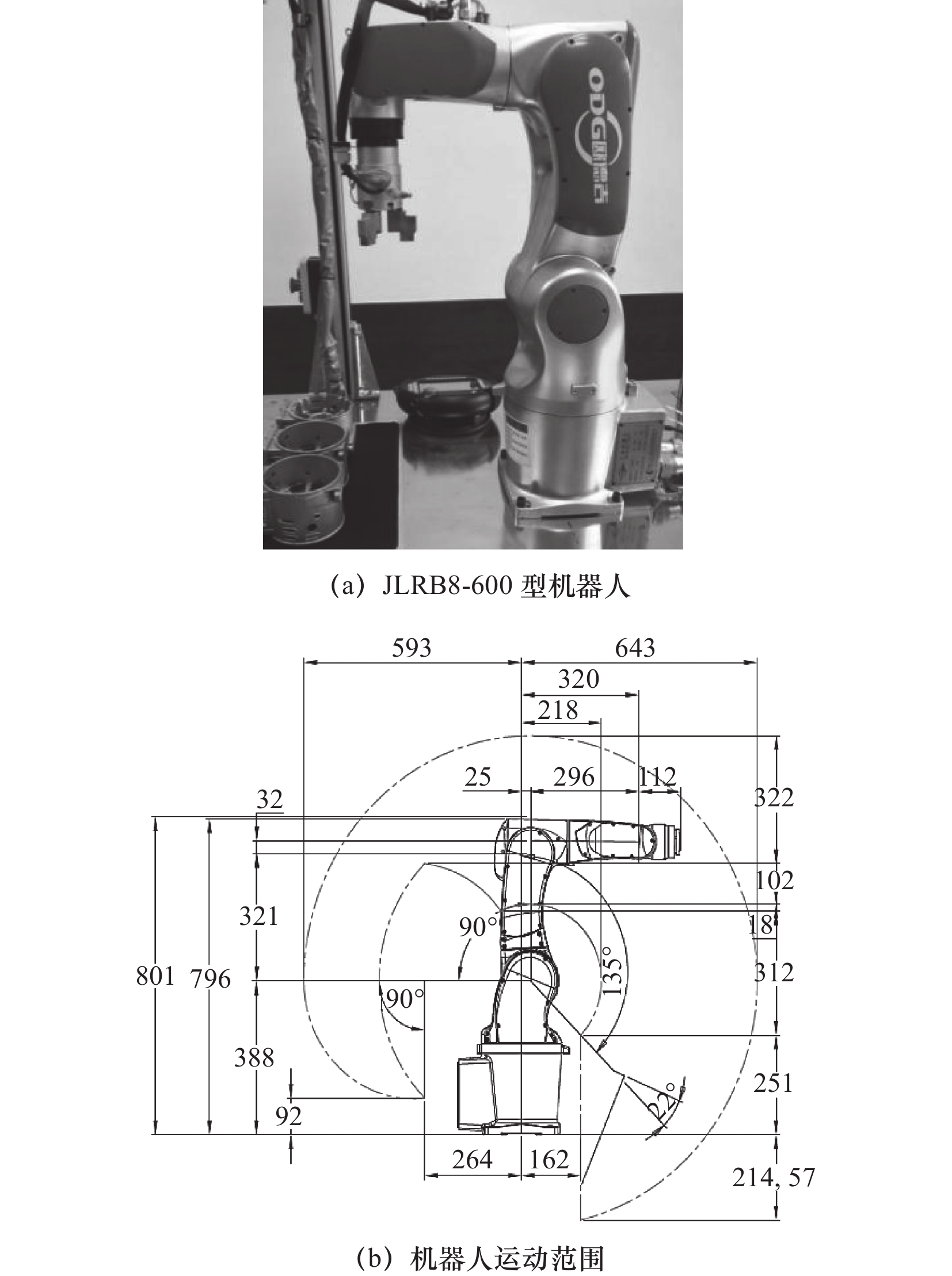
欧德吉JLRB8-600型六自由度串联机器人具有结构精巧、占地少以及重量轻的特点,其主要技术指标为:臂展长不大于1 000 mm,臂重42 kg,最大荷重8 kg,重复定位精度0.05 mm。机器人及其运动范围如图1所示。
机器人的运动学模型需满足有完备性、参数极少化和连续性的条件[6]。所以,D-H参数法被用于运动学模型的建立,只需要$ {\theta _i} $(关节转角)、$ {d_i} $(连杆偏移)、$ {a_{i - 1}} $(连杆长度)、$ {\alpha _{i - 1}} $(连杆扭转)4个运动参量就能描述机械臂关节,其D-H参数表见表1。
表 1 D-H 参数表关节 $ {\theta _i} $ $ {d_i} $ $ {a_{i - 1}} $ $ {\alpha _{i - 1}} $ 1 (−170°,170°) 387 0 0 2 (−95°,135°) 0 25 −90° 3 (−195°,70°) 0 321 0 4 (−180°,180°) 293 32 −90° 5 (−105°,105°) 0 0 90° 6 (−360°,360°) 112 0 −90° 2. 双机器人紧约束下的协调运动轨迹规划
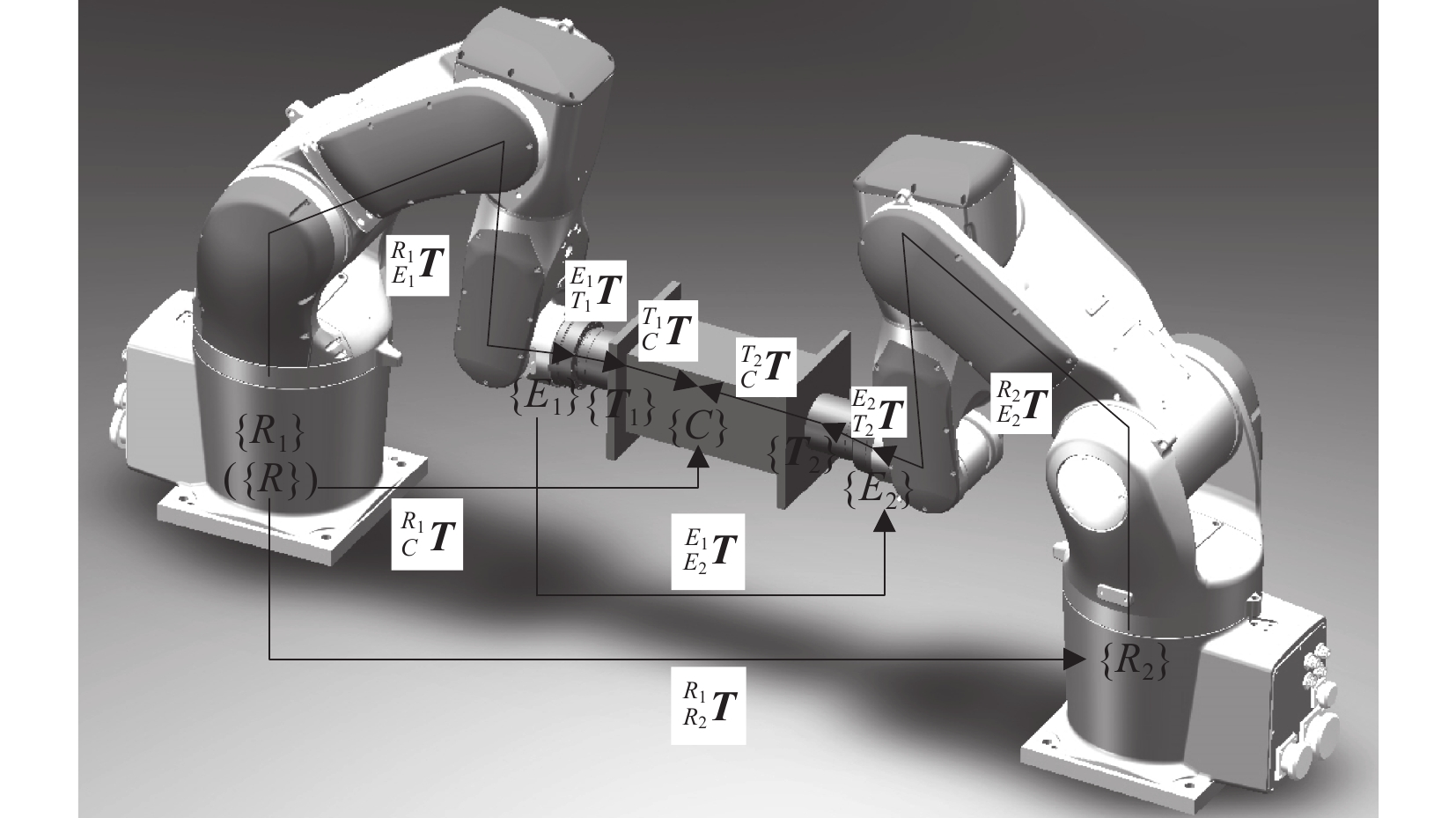
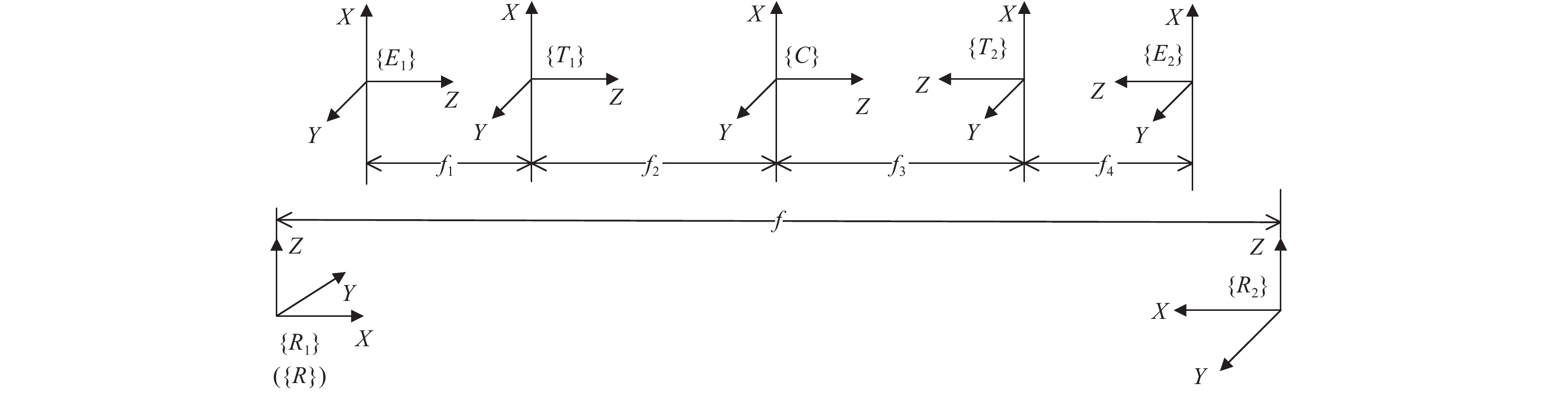
两个机械臂末端执行器在工作过程中位姿保持不变的情况称为紧约束。两个开链机器人通过紧约束形成了一个闭环运动链[7]。由底座、关节、末端、末端执行器和工件组成。在紧约束中,两个机器人不同坐标系之间的关系如图2所示,对机器人进行编号$ i $,定义世界坐标系为主机器人$ {i_1} $的基坐标系,$ \{ {R_i}\} $为机器人$ i $的基坐标系,$ \{ {E_i}\} $为机器人$ i $的末端坐标系,$ \{ {T_i}\} $为机器人$ i $的工具坐标系,$ \{ C\} $为工件的质心坐标系,$ _{E_i}^{R_i}\boldsymbol{T} $为末端坐标系到基坐标系的变换矩阵,$ _{T_i}^{E_i}\boldsymbol{T} $为末端坐标系到工具坐标系的变换矩阵,$ _C^{T_i}\boldsymbol{T} $为工具坐标系到工件质心坐标系的变换矩阵。
联合搬运的紧约束运动形成了闭环运动链:
$$ {}^{{R_1}}{{\boldsymbol{T}}_C} = {}_{{E_1}}^{{R_1}}{\boldsymbol{T}} \cdot {}_{{T_1}}^{{E_1}}{\boldsymbol{T}} \cdot {}_C^{{T_1}}{\boldsymbol{T}} = {}_{{R_2}}^{{R_1}}{\boldsymbol{T}} \cdot {}_{{E_2}}^{{R_2}}{\boldsymbol{T}} \cdot {}_{{T_2}}^{{E_2}}{\boldsymbol{T}} \cdot {}_C^{{T_2}}{\boldsymbol{T}} $$ (1) 分别右乘对应矩阵得到:
$$ {}_{{E_1}}^{{R_1}}{\boldsymbol{T}} = {}_C^{{R_1}}{\boldsymbol{T}} \cdot {({}_C^{{T_1}}{\boldsymbol{T}})^{ - 1}} \cdot {({}_{{T_1}}^{{E_1}}{\boldsymbol{T}})^{ - 1}} $$ (2) 机器人$ {i_1} $的基坐标系到末端坐标系的变换矩阵可由等号右边求得,逆运动学分析可获得各关节的角位移。已知$ _{T_1}^{E_1}\boldsymbol{T} $和$ _C^{T_1}\boldsymbol{T} $,通过示教得出工件在机器人$ {i_1} $基坐标下的运动轨迹为$ _C^{R_1}\boldsymbol{T} $。
因为紧约束下机器人末端的位姿是不变的,已知$ _{E_2}^{E_1}\boldsymbol{T} $,所以:
$$ {}_{{E_2}}^{{E_1}}{\boldsymbol{T}} = {}_{{T_1}}^{{E_1}}{\boldsymbol{T}} \cdot {}_C^{{T_1}}{\boldsymbol{T}} \cdot {}_{{T_2}}^C{\boldsymbol{T}} \cdot {}_{{E_2}}^{{T_2}}{\boldsymbol{T}} $$ (3) 式(3)中都是常数矩阵,结合式(1)有:
$$ {}_{{E_1}}^{{R_1}}{\boldsymbol{T}} \cdot {}_{{E_2}}^{{E_1}}{\boldsymbol{T}} = {}_{{R_2}}^{{R_1}}{\boldsymbol{T}} \cdot {}_{{E_2}}^{{R_2}}{\boldsymbol{T}} $$ (4) 左乘对应矩阵得:
$$ {}_{{E_2}}^{{R_2}}{\boldsymbol{T}} = {({}_{{R_2}}^{{R_1}}{\boldsymbol{T}})^{ - 1}} \cdot {}_{{E_1}}^{{R_1}}{\boldsymbol{T }}\cdot {}_{{E_2}}^{{E_1}}{\boldsymbol{T}} $$ (5) 通过标定获得两机器人的基坐标系之间变换矩阵$ _{R_2}^{R_1}\boldsymbol{T} $;由式(2)得$ _{E_1}^{R_1}\boldsymbol{T} $;当任务确定时,$ _{E_2}^{E_1}\boldsymbol{\boldsymbol{ }T} $的值也是确定的;这样就可求出$ _{E_2}^{R_2}\boldsymbol{T} $,由逆运动学得到机器人$ {i_2} $的角位移,驱动机器人运动。
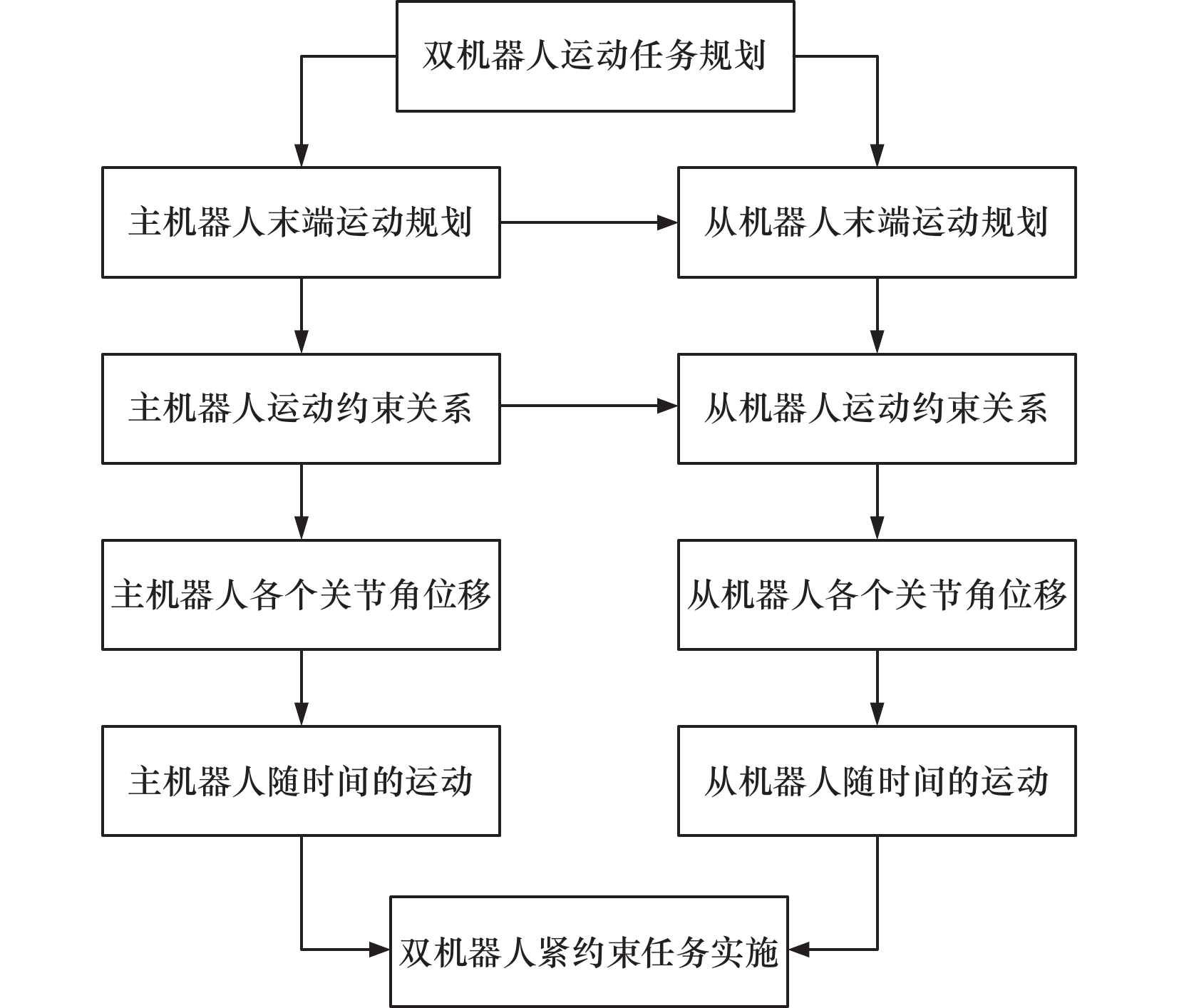
机器人$ {i_1} $与$ {i_2} $的$ _{E_i}^{R_i}\boldsymbol{T} $是随时间变化的函数矩阵,式(5)中$ _{E_2}^{R_2}\boldsymbol{T} $可根据$ _{E_1}^{R_1}\boldsymbol{T} $解得,这样就可以实现机器人$ {i_1} $与$ {i_2} $在时间上的同步。紧约束运动学原理如图3所示。
3. 双机器人松约束下的协调运动轨迹规划
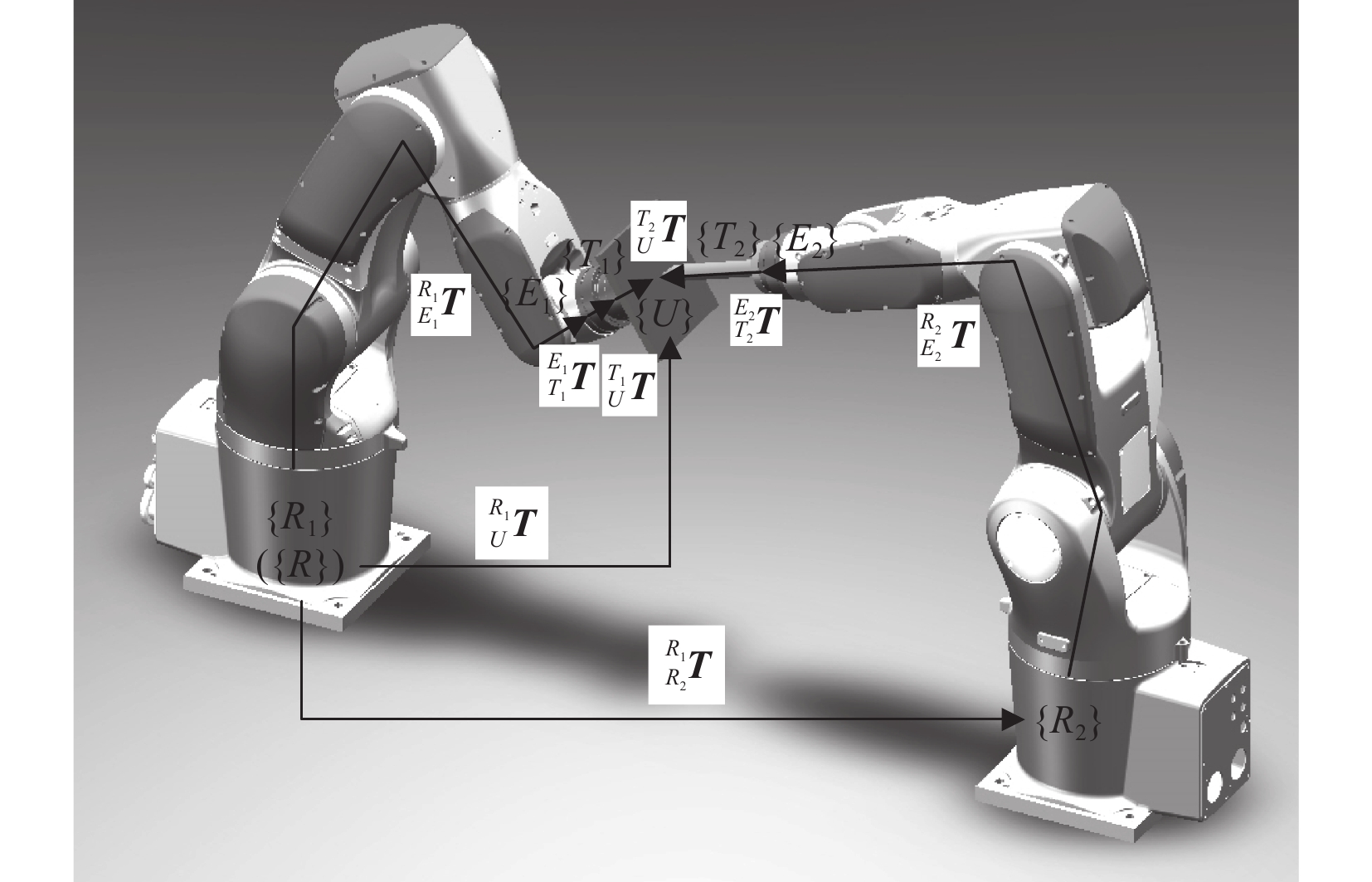
松约束运动中机器人末端的相对位姿因任务的不同而发生变化[8]。设世界坐标系与机器人$ {i_1} $基坐标系重合,即$ \{ R\} = \{ {R_1}\} $,$ \{ U\} $代表工件坐标系,将其定义在被$ {i_2} $末端执行器夹持固定的工件上,$ _U^{T_i}\boldsymbol{T} $是工具坐标系到工件坐标系的变换矩阵。松约束中各坐标系关系如图4所示。
双机器人松约束运动中,仍有一条闭环运动链,这条运动链从世界坐标系,即主机器人的基本坐标系出发,再将两个机器人的身体分割成两个部分,最后汇合在一起,形成一个闭环[9]。因此,可以推导出主从机之间的关系:
$$ _U^R\boldsymbol{T}=_U^{R_1}\boldsymbol{T}=_{E_1}^{R_1}\boldsymbol{T}\cdot_{T_1}^{E_1}\boldsymbol{T}\cdot_U^{T_1}\boldsymbol{T} $$ (6) $$ _U^R\boldsymbol{T}=_U^{R_1}\boldsymbol{T}=_{R_2}^{R_1}\boldsymbol{T}\cdot_{E_2}^{R_2}\boldsymbol{T}\cdot_{T_2}^{E_2}\boldsymbol{T}\cdot_U^{T_2}\boldsymbol{T} $$ (7) 式(6)和式(7)是从基础坐标到工具坐标的主、从机器人的运动链,可以得到以下关系:
$$ _{E_1}^{R_1}\boldsymbol{T}=_U^{R_1}\boldsymbol{T}\cdot(_U^{T_1}\boldsymbol{T})^{-1}\cdot(_{T_1}^{E_1}\boldsymbol{T})^{-1} $$ (8) $$ _{E_2}^{R_2}\boldsymbol{T}=(_{R_2}^{R_1}\boldsymbol{T})^{-1}\cdot_U^{R_1}\boldsymbol{T}\cdot(_U^{T_2}\boldsymbol{T})^{-1}\cdot(_{T_2}^{E_2}\boldsymbol{T})^{-1} $$ (9) 通过分析可以看出,式(8)和式(9)中右边除了$ _U^{R_1}\boldsymbol{T} $之外均为常数,$ _U^{R_1}\boldsymbol{T} $是时变函数矩阵,所以$ _{E_1}^{R_1}\boldsymbol{T} $和$ _{E_2}^{R_2}\boldsymbol{T} $也是时变函数矩阵。然后根据逆运动学原理,求出各个关节的角位移,实现了主从机械臂的动作。
4. 仿真实验分析
4.1 紧约束下的Matlab双机器人轨迹验证
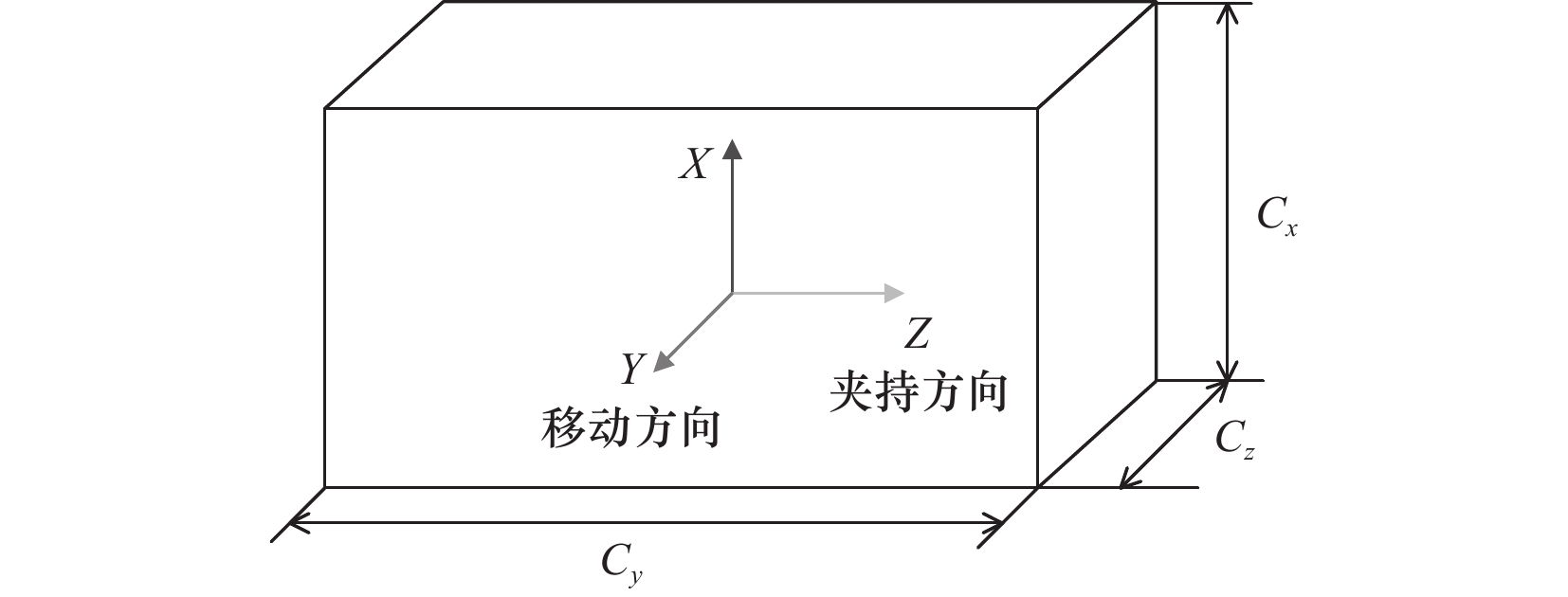
假定工件C的尺寸为$ {{\text{C}}_x} \times {{\text{C}}_y} \times {{\text{C}}_z} $(单位为mm),质心与工件坐标系$ \{ C\} $原点重合,位于中心位置,$ Z $轴沿机器人$ {i_1} $基坐标系$ X $轴方向,$ X $轴竖直向上,$ Y $轴由右手法则确定,如图5所示。
图6显示了在两个机械手的紧约束中不同部分的坐标系信息。将任务目标设置为:机器人在两边搬运工件$ C $,定义起点$ A $,终点$ B $,总长$ L $,$ {i_1} $在左、$ {i_2} $在右,二者沿世界坐标系轴$ x $相对立,搬运过程中,二者相对速度为零。得到工件$ C $与世界坐标系的变换矩阵为
$$ {}_C^{{R_1}}{{\boldsymbol{T}}_{\text{1}}} = \left[ {\begin{array}{*{20}{c}} {}&{{A_x} + \Delta {l_x}} \\ {{\mathrm{Rot}}({\textit{z}},0) \cdot {\mathrm{Rot}}(x,180^\circ ) \cdot {\mathrm{Rot}}(y,90^\circ )}&{{A_y} + \Delta {l_y}} \\ {}&{{A_{\textit{z}}} + \Delta {l_{\textit{z}}}} \\ {0\begin{array}{*{20}{c}} {}&{0\begin{array}{*{20}{c}} {}&0 \end{array}} \end{array}}&1 \end{array}} \right] $$ (10) 在紧约束下,机器人$ {i_1} $与$ {i_2} $夹持工具相对于机器人末端的变换矩阵为
$$ {}_{{T_1}}^{{E_1}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&{{f_1}} \\ 0&0&0&1 \end{array}} \right] \quad {}_{{T_{\text{2}}}}^{{E_{\text{2}}}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&{{f_{\text{4}}}} \\ 0&0&0&1 \end{array}} \right] $$ (11) 在搬运过程中,工件相对机器人$ {i_1} $与$ {i_2} $工具坐标系变换矩阵为
$$ {}_C^{{T_1}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&{{f_2}} \\ 0&0&0&1 \end{array}} \right]\quad {}_C^{{T_2}}{\boldsymbol{T }}= \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{ - 1}&0&0 \\ 0&0&{ - 1}&{{f_3}} \\ 0&0&0&1 \end{array}} \right] $$ (12) 设置从机器人基坐标系相对于世界坐标系的位置为
$$ {}_{{R_{\text{2}}}}^{{R_{\text{1}}}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {}&f \\ {{\mathrm{Rot}}({\textit{z}},180^\circ ) \cdot {\mathrm{Rot}}(x,0) \cdot {\mathrm{Rot}}(y,0)}&{\text{0}} \\ {}&{\text{0}} \\ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}} \end{array}}&1 \end{array}} \right] $$ (13) 根据式(2)可以得出$ {i_1} $末端相对于基坐标系的变换矩阵:
$$ {}_{{E_1}}^{{R_1}}{\boldsymbol{T}} = {}_C^{{R_1}}{\boldsymbol{T}} \cdot {({}_C^{{T_1}}{\boldsymbol{T}})^{ - 1}} \cdot {({}_{{T_1}}^{{E_1}}{\boldsymbol{T}})^{ - 1}} = \left[ {\begin{array}{*{20}{c}} 0&0&1&{{A_x} + \Delta {l_x} + {f_1} - {f_2}} \\ 0&{ - 1}&0&{{A_y} + \Delta {l_y}} \\ 1&0&0&{{A_{\textit{z}}} + \Delta {l_{\textit{z}}}} \\ 0&0&0&1 \end{array}} \right] $$ (14) 由于两机器人末端的位姿不发生变化,由式(3)得:
$$ {}_{{E_2}}^{{E_1}}{\boldsymbol{T }}= {}_{{T_1}}^{{E_1}}{\boldsymbol{T}} \cdot {}_C^{{T_1}}{\boldsymbol{T}} \cdot {}_{{T_2}}^C{\boldsymbol{T}} \cdot {}_{{E_2}}^{{T_2}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{ - 1}&0&0 \\ 0&0&{ - 1}&{{f_1} + {f_2} + {f_3} + {f_4}} \\ 0&0&0&1 \end{array}} \right] $$ (15) 根据(5)可得机器人$ {i_2} $末端到基坐标系的变换矩阵:
$$\begin{split} & {}_{{E_2}}^{{R_2}}{\boldsymbol{T}} = {({}_{{R_2}}^{{R_1}}{\boldsymbol{T}})^{ - 1}} \cdot {}_{{E_1}}^{{R_1}}{\boldsymbol{T}} \cdot {}_{{E_2}}^{{E_1}}{\boldsymbol{T}} = \\ &\left[ {\begin{array}{*{20}{c}} 0&0&1&{f - {A_x} - \Delta {l_x} - 2{f_1} - {f_3} - {f_4}} \\ 0&{ - 1}&0&{ - {A_y} - \Delta {l_y}} \\ 1&0&0&{{A_{\textit{z}}} + \Delta {l_{\textit{z}}}} \\ 0&0&0&1 \end{array}} \right] \end{split} $$ (16) 由式(14)和式(16),可得机器人$ {i_1} $与$ {i_2} $末端相对基坐标系的变换矩阵,再通过逆运动学求出各关节的角位移,从而实现机械臂的动作。
在 Matlab的基础上,将上述双机器人协调搬运参数设定为:$ A = [400,250,200] $、$ B = [400, - 250,200] $,工件C轮廓尺寸$ 100\ \mathrm{mm}\times100\ \mathrm{mm}\times200\text{ mm} $,工件质心与末端坐标系原点保持水平,有$ f_2=f_3=100\text{ mm} $,起点为A,终点为B,$ {i_1} $与$ {i_2} $的工具有效长度为$ f_1= f_4=50\ \text{mm} $,设置$ f=1\ 000\text{ mm} $。上面的数值被替换到式(14)~式(16)中仿真。
Matlab因其良好的运算性能而被广泛应用[10]。利用 Matlab中的Robotic Toolbox对两个机器人在动画层面上的动作进行了模拟和分析。该工具箱是澳洲学者Peter Corke发明的,用来研究和模拟关节型和移动型的机器人,里面包含了一些关于机器人的基础算法的函数,有一些比较成熟的代码,可以很直观地显示出编写的程序。
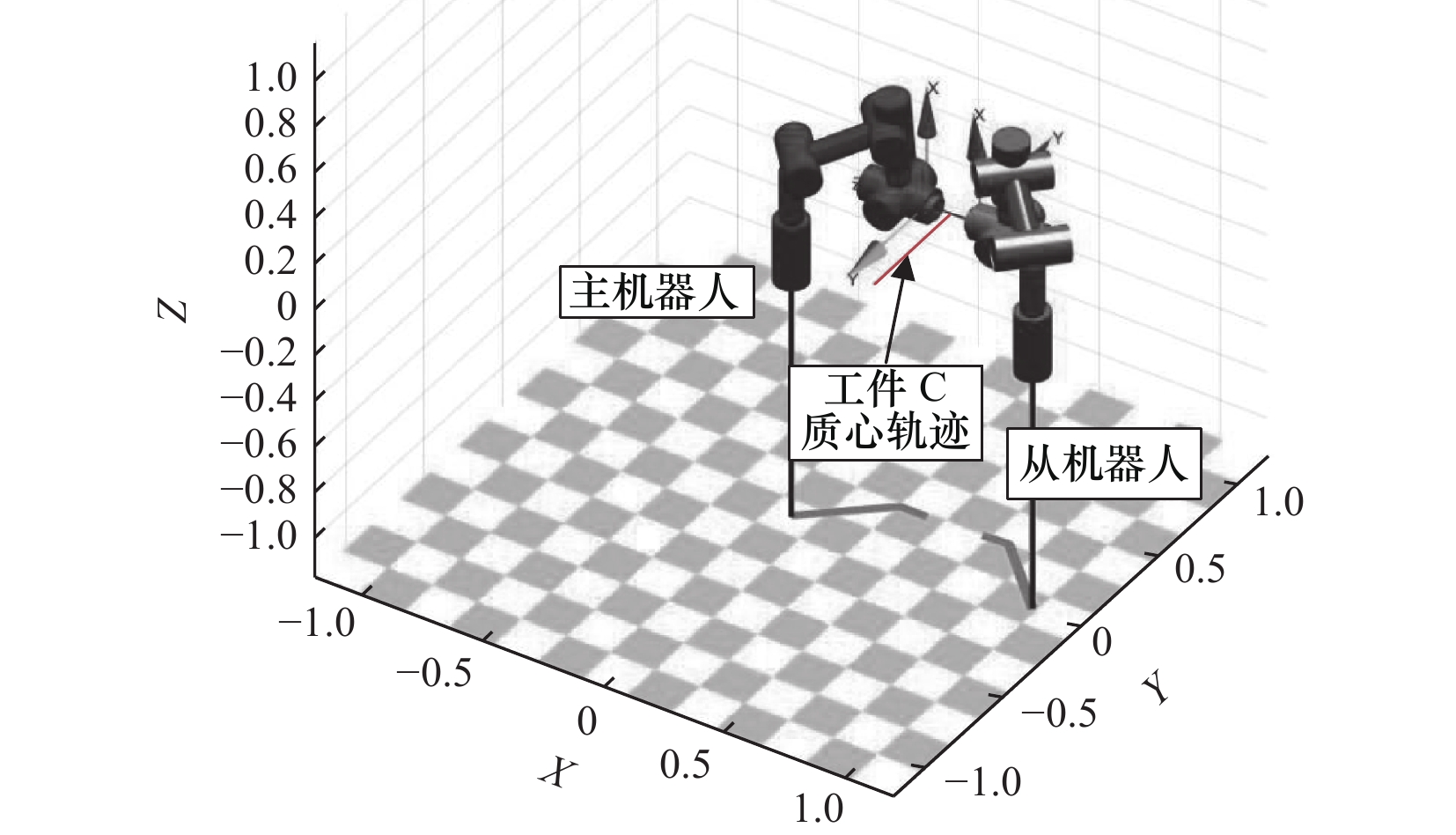
图7所示为用 Matlab软件实现的两台机械臂协同操作的模拟原理图。
红线表示工件C的轨迹,基座在世界坐标系沿轴线X相对放置,由此可以看出,两台机器人的末端X方向是相同的,轴线Y与轴线Z方向相反。
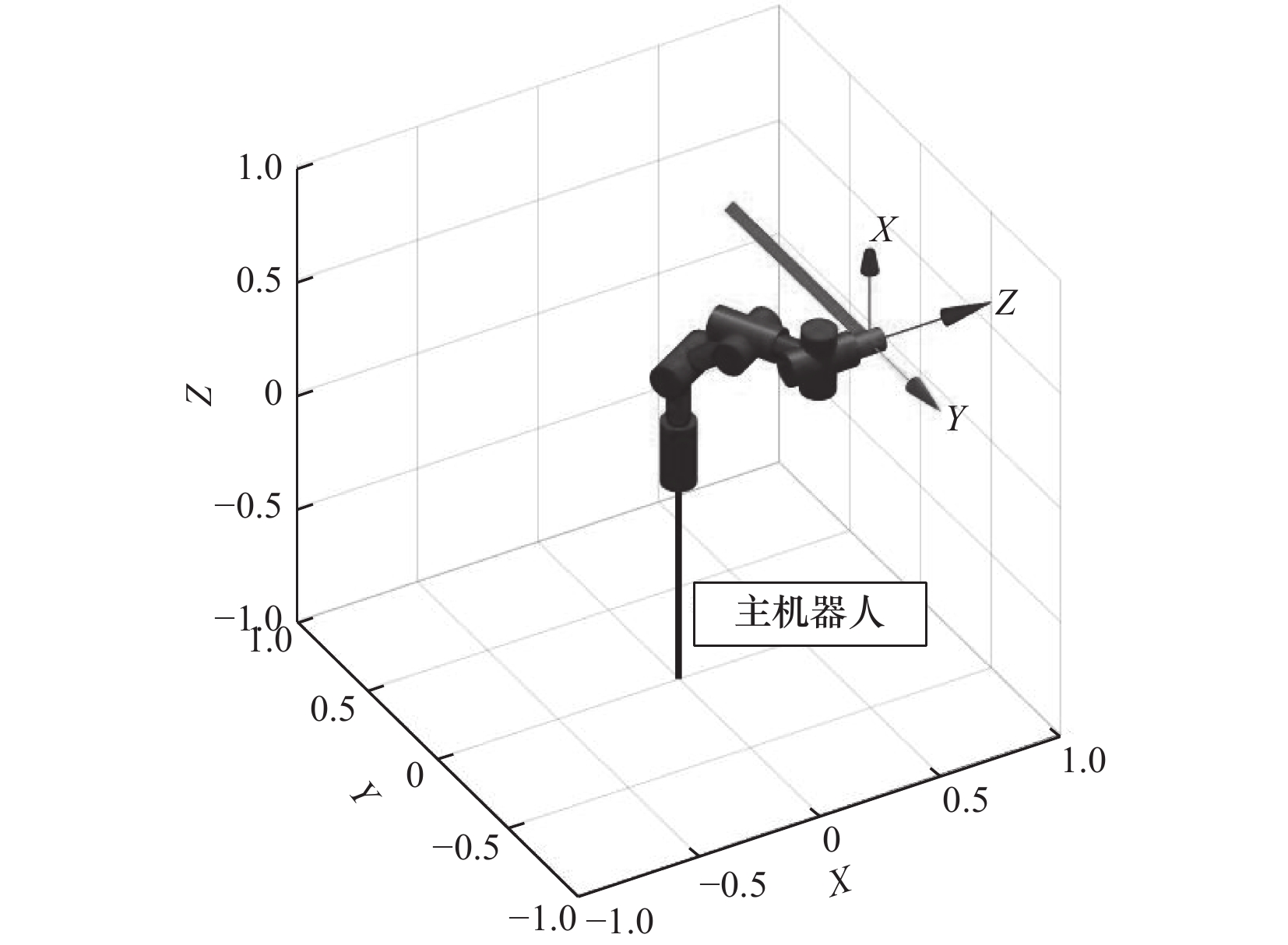
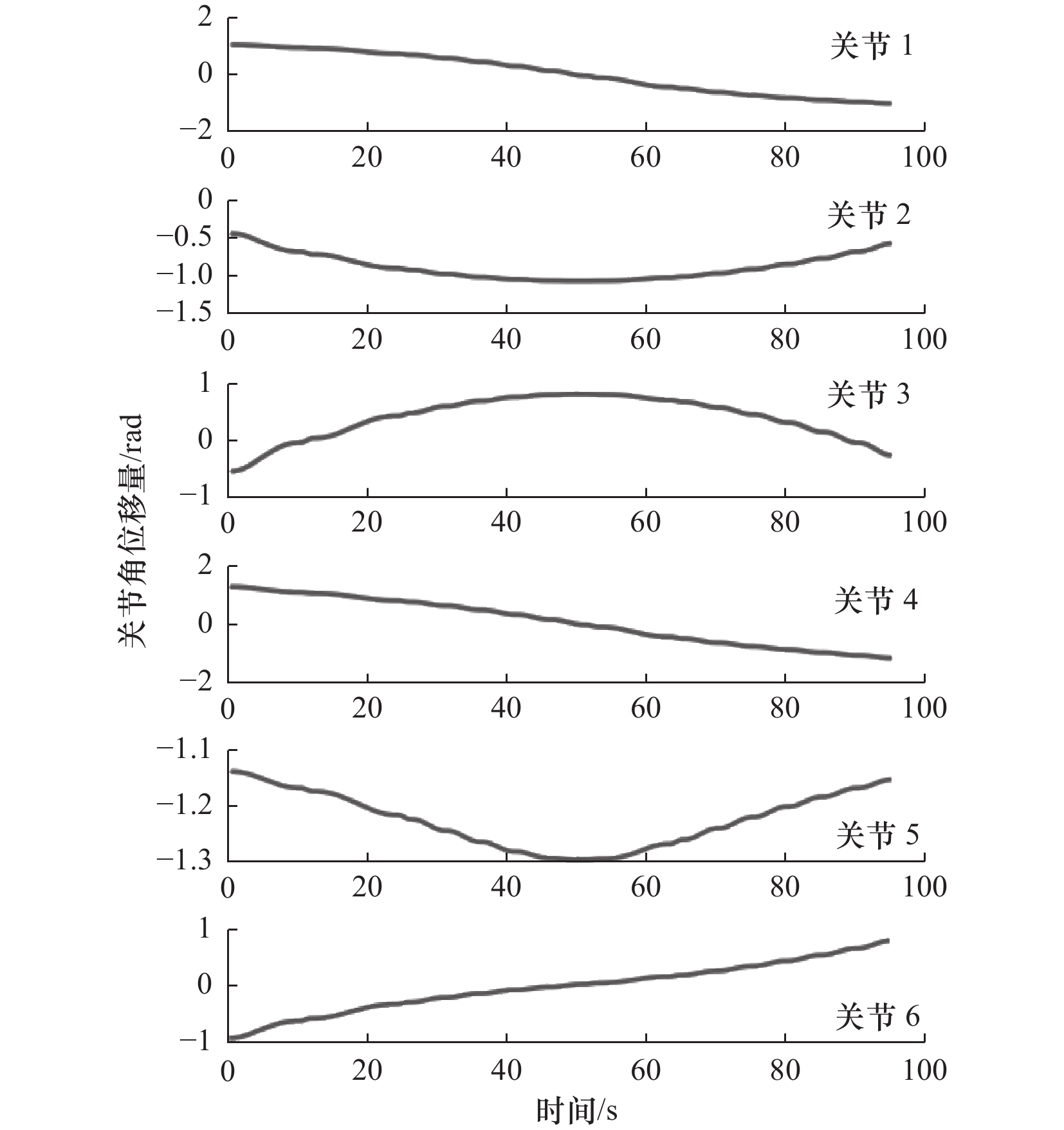
图8所示为主机器人的轨迹,此时动作已经结束,末端执行器的轨迹为直线,运动过程中末端位姿不发生变化,移动距离为$ 500\;{\text{mm}} $。图9所示为主机器人各关节的角位移。
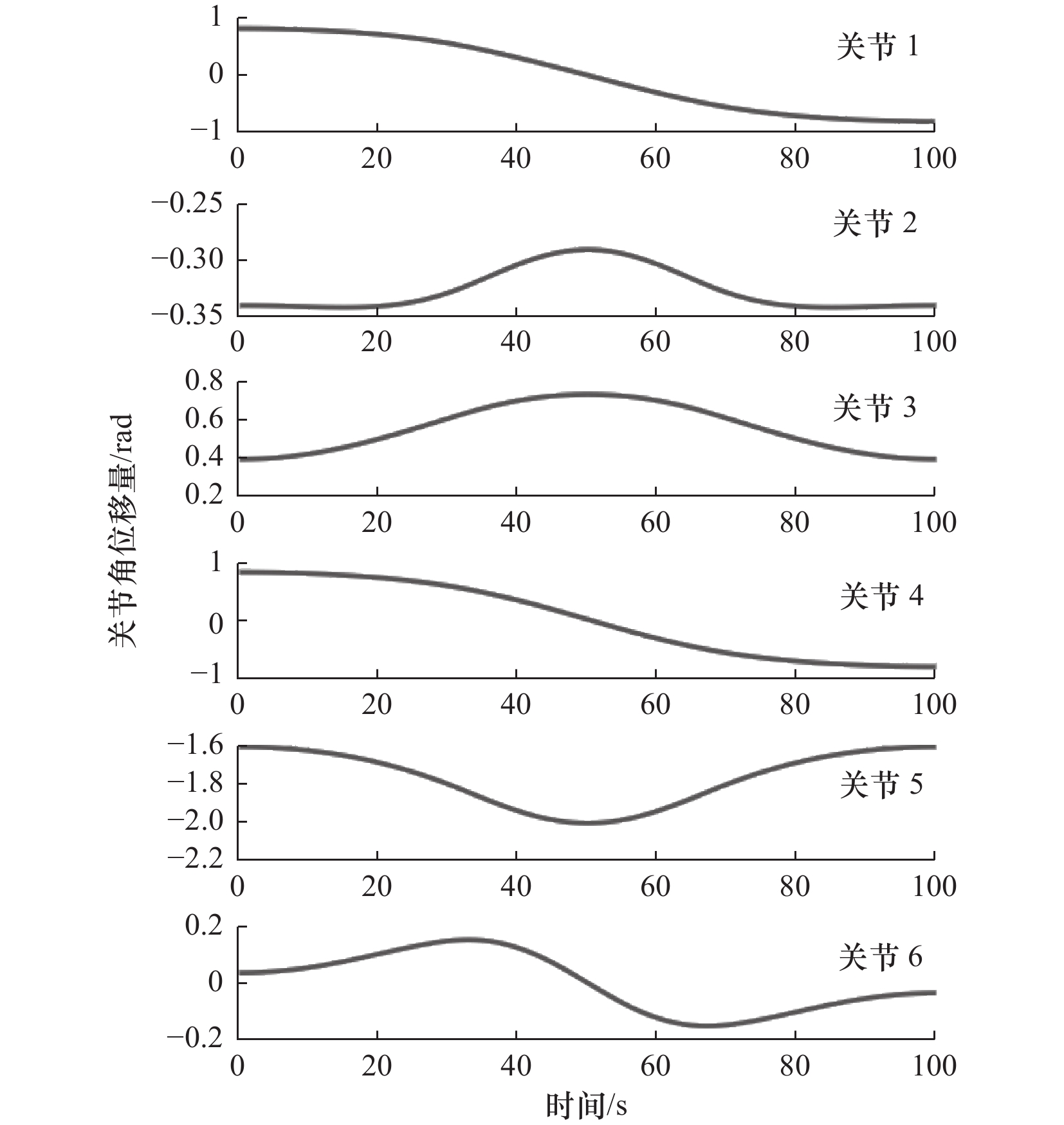
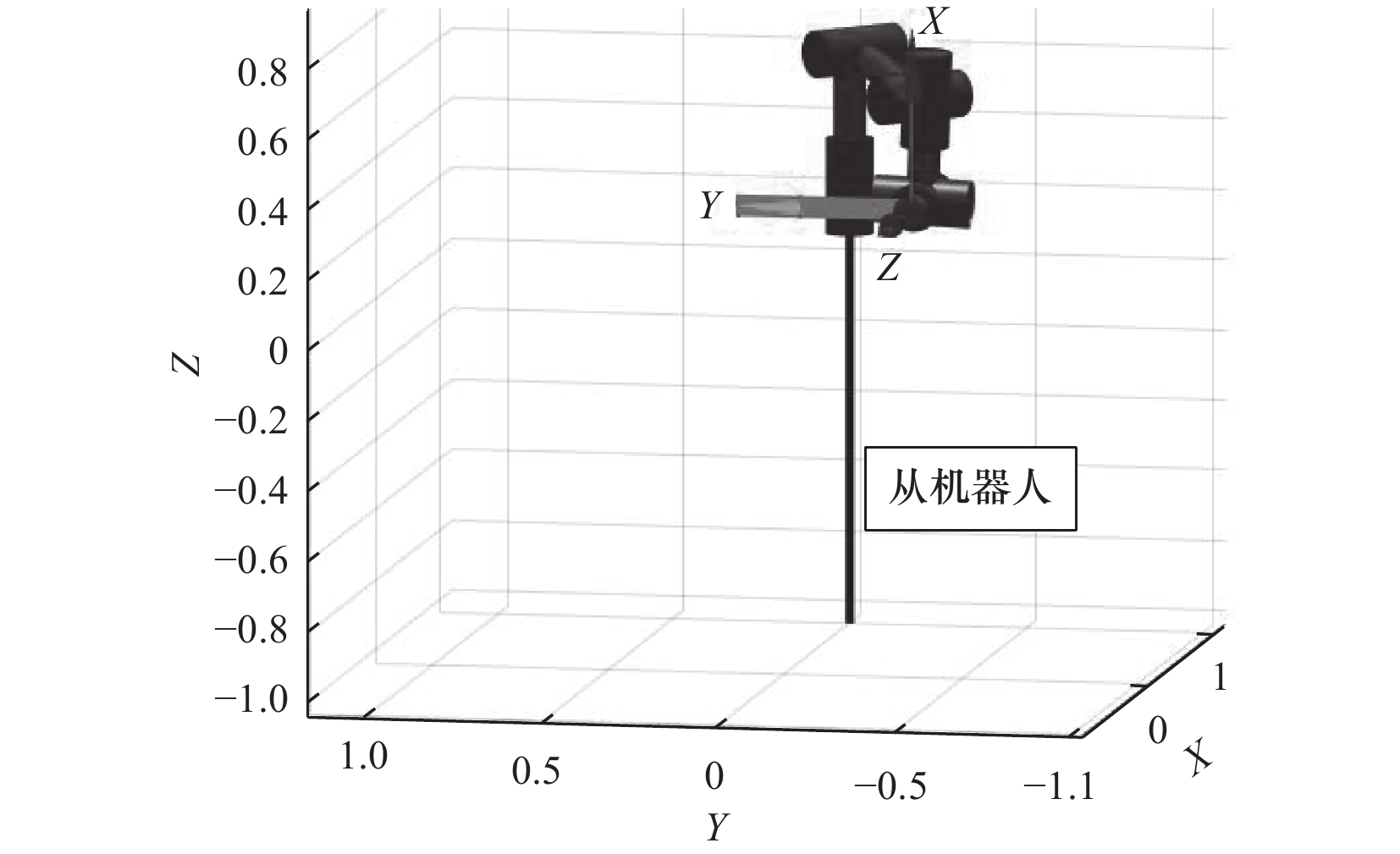
对于机器人$ {i_2} $,基坐标原点位于$ [1000,0,0] $,X轴与世界坐标系X轴方向相反,运动轨迹总长$ 500\ \text{mm} $,$ {i_2} $的末端轨迹如图10所示,$ {i_2} $的各关节的角位移如图11所示。
仿真结果与预定参数一致,各关节运动相对平缓,无明显拐点,机器人的动作平稳顺畅,验证了该方法的正确性和有效性。
4.2 松约束下的Matlab双机器人轨迹验证
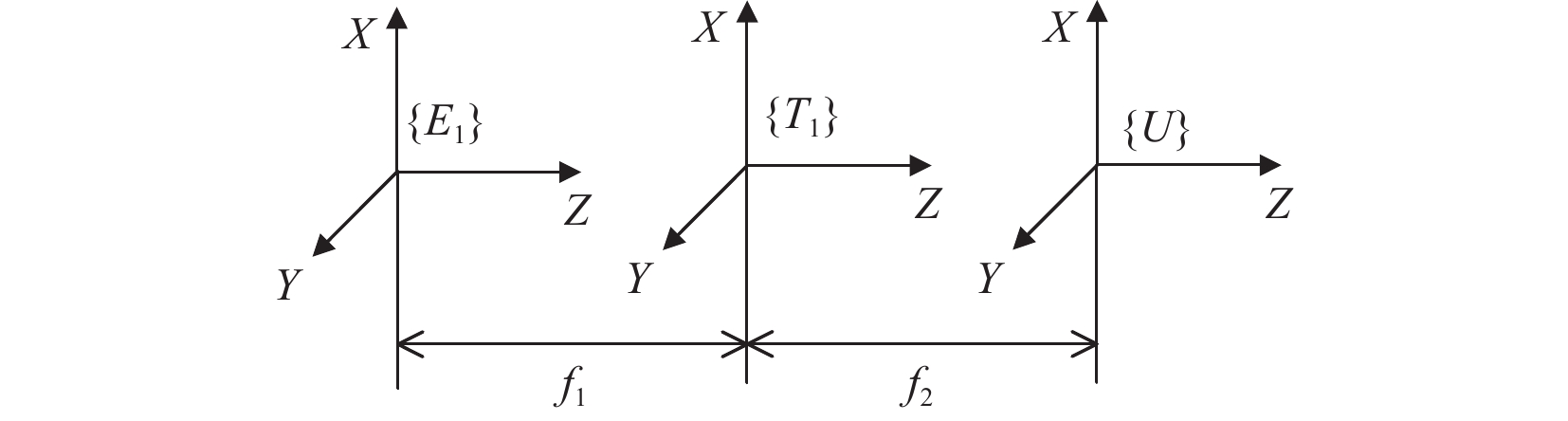
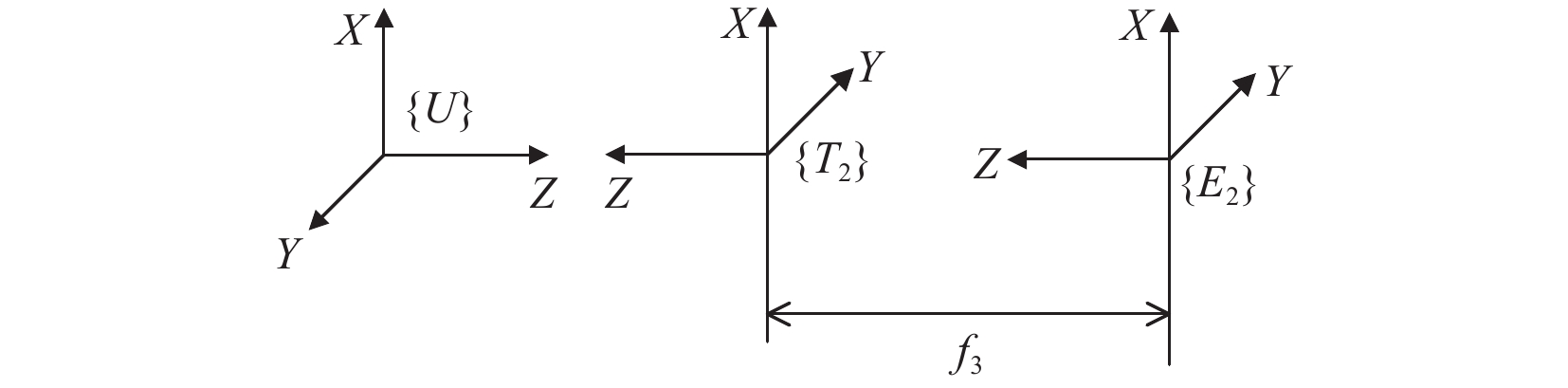
在协同写字过程中,使机器人$ {i_1} $夹持书写板,机器人$ {i_2} $夹持书写笔;写字板变速移动,写字笔书写“123”字体,并随着写字板移动,如图12所示;定义工件坐标系$ \{ U\} $的原点在写字板中心,$ {i_2} $工具坐标系$ {\text{\{ }}T{}_2{\text{\} }} $原点在写字笔的顶端,图13和图14分别为各坐标系相对位置关系,仍按图6设置$ {i_1} $与$ {i_2} $的基坐标系。
$ {i_1} $的末端、工具和工件坐标系如图13所示。
$ {i_2} $的末端、工具和工件坐标系如图14所示。
设$ {i_1} $基坐标系与世界坐标系重合,在主基坐标系中,起点为A$ [{A_x},{A_y},{A_{\textit{z}}}] $,终点为B$ [{B_x},{B_y},{B_{\textit{z}}}] $,总长$ l_{\text{1}} $。$ {i_1} $的运动路径确定后,即可推导出$ {i_2} $的运动路径及相关参数。
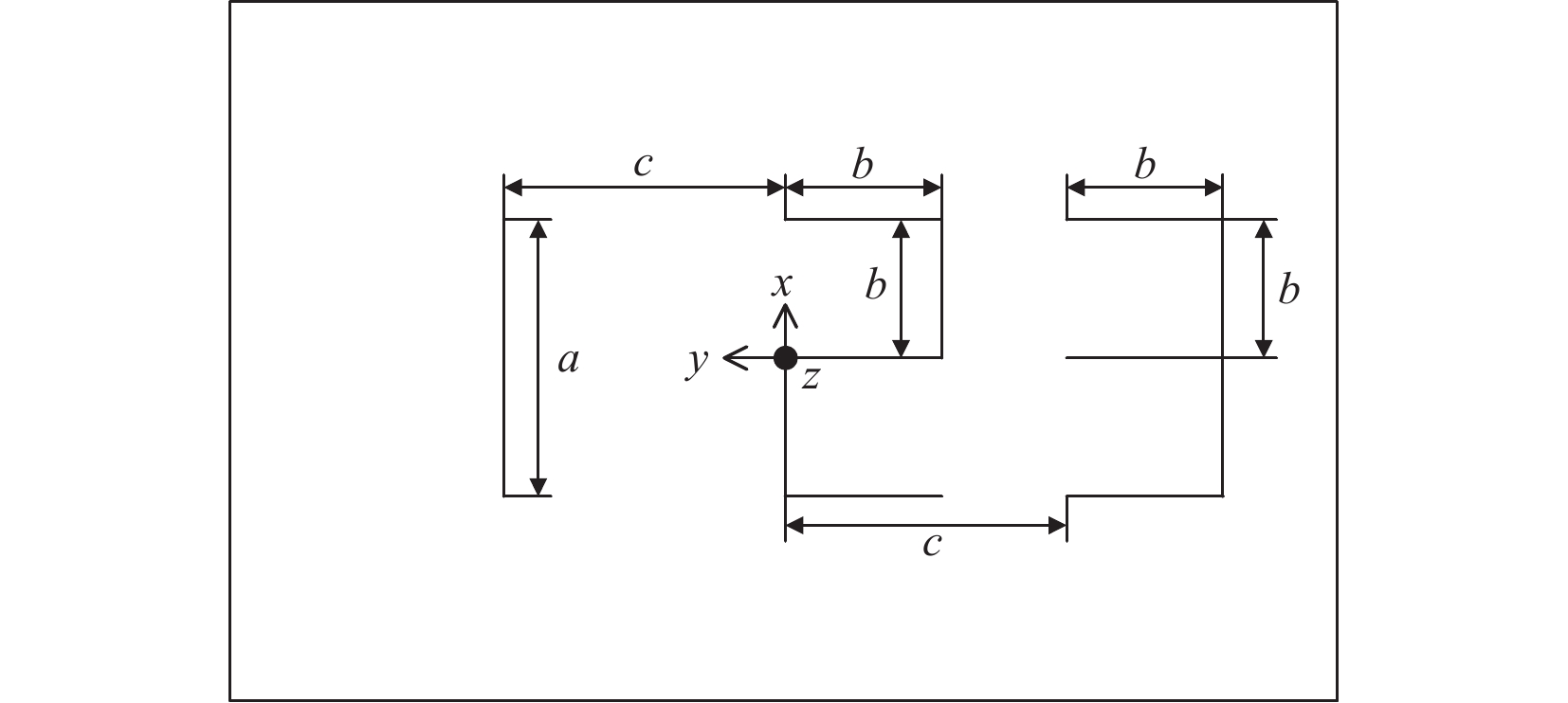
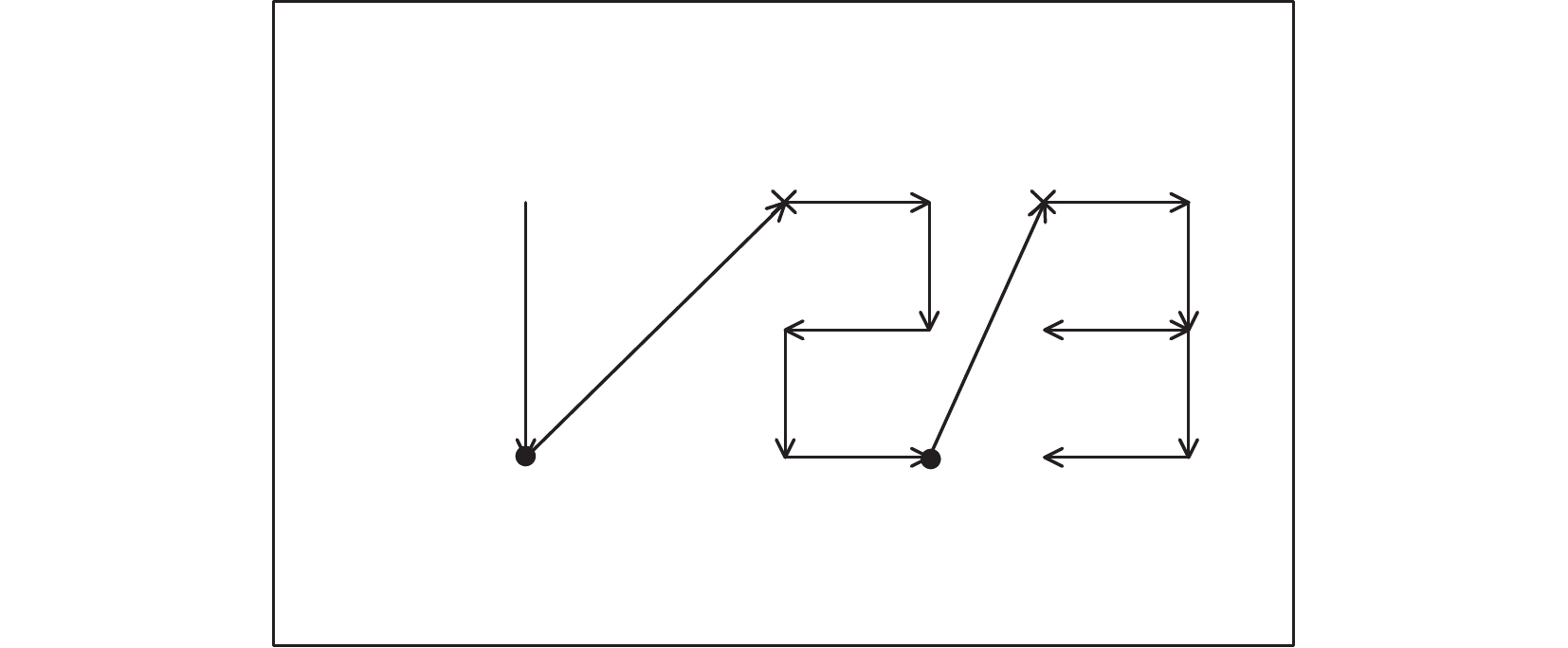
写字的过程中,规定从左到右,从上到下,一笔写完一个字,写完后抬笔移到下一个位置。每个字的起始位置为左上角,写字笔的理想路径如图15所示。设抬笔高度为$ d $,计算得写字总长度$ {l_2} $为
$$ {l_2} = a + 4d + 11b + \sqrt {{a^2} + {c^2}} + \sqrt {{a^2} + {{(c - b)}^2}} $$ (17) 以式(8)和式(9)为基础,得到$ {i_1} $与$ {i_2} $末端相对基坐标的关系等式。从图4中可以看出,在松约束下中,$ {i_1} $工具坐标系、基坐标系分别与工件坐标系之间的变换矩阵:
$$ _U^{T_1}\boldsymbol{T}=\left[\begin{array}{*{20}{c}}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & f_{\text{2}} \\ 0 & 0 & 0 & 1\end{array}\right] $$ (18) $$ _U^{R_1}\boldsymbol{T}=\left[\begin{array}{*{20}{c}} & A_x+\Delta a_x \\ {{\mathrm{Rot}}}({\textit{z}},0)\cdot{{\mathrm{Rot}}}(x,180^{\circ})\cdot{{\mathrm{Rot}}}(y,90^{\circ}) & A_y+\Delta a_y \\ & A_{{\textit{z}}}+\Delta a_{{\textit{z}}} \\ 0\begin{array}{*{20}{c}} & 0\begin{array}{*{20}{c}} & 0\end{array}\end{array} & 1\end{array}\right] $$ (19) $ \Delta {a_i}(i = x,y,{\textit{z}}) $是写字板移动过程中与写字笔所需的距离,该数值有正负之分。
$ {i_1} $末端与工具坐标系的关系矩阵:
$$ _{T_1}^{E_1}\boldsymbol{T}=\left[\begin{array}{*{20}{c}}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & f_{\text{1}} \\ 0 & 0 & 0 & 1\end{array}\right] $$ (20) 由式(8)、式(18)、式(19)和式(20)可得$ {i_1} $末端相对基坐标系的变换矩阵,逆运动学求出各关节角位移,使机器人到达相应位置:
$$ _{E_1}^{R_1}\boldsymbol{T}=_U^{R_1}\boldsymbol{T}\cdot(_U^{T_1}\boldsymbol{T})^{-1}\cdot(_{T_1}^{E_1}\boldsymbol{T})^{-1}=\left[\begin{array}{*{20}{c}}0 & 0 & 1 & A_x+\Delta a_x-f_1-f_2 \\ 0 & -1 & 0 & A_y+\Delta a_y \\ 1 & 0 & 0 & A_{\textit{z}}+\Delta a_{\textit{z}} \\ 0 & 0 & 0 & 1\end{array}\right] $$ (21) $ {i_2} $末端与写字笔工具坐标系之间的关系:
$$ _{T_2}^{E_2}\boldsymbol{T}=\left[\begin{array}{*{20}{c}}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & f_3 \\ 0 & 0 & 0 & 1\end{array}\right] $$ (22) 写字笔工具坐标系与写字板工件坐标系的关系为
$$ _U^{T_2}\boldsymbol{T}=\left[\begin{array}{*{20}{c}} & p_i=p_{i-1}+\Delta l_{xi} \\ {{\mathrm{Rot}}}({\textit{z}},0)\cdot{{\mathrm{Rot}}}(x,180^{\circ})\cdot{{\mathrm{Rot}}}(y,0) & q_i=q_{i-1}+\Delta l_{yi} \\ & w_i=w_{i-1}+\Delta l_{{\textit{z}}i} \\ \begin{array}{*{20}{c}}0 & 0 & 0\end{array} & 1\end{array}\right] $$ (23) $ \Delta l $为写字笔在轴上的移动距离,$ [{p_i},{q_i},{w_i}] $是工件坐标系相对工具坐标在某一时刻的位置,与书写内容和顺序有关。由图15可以看出,完成这一任务共需18笔,而“3”中只有1次重复。因此可以得出笔的书写过程是由18个点来控制的结论,也就是说$ i=\mathrm{2,3},4,\cdots ,i\geqslant 18 $,$ i = 1 $时是起始位置,$ [{p_1},{q_1},{w_1}] = \left[ - \dfrac{a}{2},c,0\right] $是$ {i_2} $工具坐标系中书写开始点。
假设世界坐标系与$ {i_1} $基坐标系重合,那么$ {i_2} $与世界坐标系的关系就可以确定:
$$ _{R_{\text{2}}}^{R_{\text{1}}}\boldsymbol{T}=\left[\begin{array}{*{20}{c}} & f \\ {{\mathrm{Rot}}}({\textit{z}},180^{\circ})\cdot{{\mathrm{Rot}}}(x,0)\cdot{{\mathrm{Rot}}}(y,0) & \text{0} \\ & \text{0} \\ \begin{array}{*{20}{c}}\text{0} & \text{0} & \text{0}\end{array} & 1\end{array}\right] $$ (24) 据式(8)、式(19)、式(22)、式(23)、式(24),$ {i_2} $末端相对基坐标系的变换矩阵为
$$ \begin{split} & _{E_{\text{2}}}^{R_{\text{2}}}\boldsymbol{T}=(_{R_2}^{R_1}\boldsymbol{T})^{-1}\cdot_U^{R_1}\boldsymbol{T}\cdot(_U^{T_2}\boldsymbol{T})^{-1}\cdot(_{T_2}^{E_2}\boldsymbol{T})^{-1}= \\ & \left[\begin{array}{*{20}{c}}0 & 0 & 1 & f-A_x-\Delta a_x-f_3-w_i \\ 0 & -1 & 0 & q_i-A_y-\Delta a_y \\ 1 & 0 & 0 & A_{\text{z}}+\Delta a_{\text{z}}-p_i \\ 0 & 0 & 0 & 1\end{array}\right]\end{split} $$ (25) 式中,仅$ {}_U^{{R_1}}T $与$ {}_U^{{T_2}}T $是变量,其数值会对$ {i_2} $末端的位姿产生影响,而$ [\Delta {a_x},\Delta {a_y},\Delta {a_{\textit{z}}}] $与$ [\Delta {l_{xi}},\Delta {l_{yi}},\Delta {l_{{\textit{z}}i}}] $会决定它们的数值,二者分别是相对于世界坐标系和$ {i_2} $工具坐标系中各方向的变量,即在一定的时间内两绝对值相等。由式(21)和式(25)可得两机器人末端位姿,再通过机器人逆运动学求解得到$ {i_2} $在书写各点时关节的角位移,驱动机器人运动。
假设各参数为
$$ \left\{ {\begin{array}{*{20}{l}} {{f_1} = 40\;{\text{mm}}} \\ {{f_2} = 60\;{\text{mm}}} \\ {{f_3} = 142\;{\text{mm}}} \\ {f = 1000\;{\text{mm}}} \end{array}} \right. $$ $$ \left\{ {\begin{array}{*{20}{l}} {A = [500,500,600]} \\ {B = [500, - 500,600]} \\ {{l_1} = 1000\;{\text{mm}}} \end{array}} \right. $$ $$ \left\{ {\begin{array}{*{20}{l}} {a = 100\;{\text{mm}}} \\ {b = 50\;{\text{mm}}} \\ {c = 80\;{\text{mm}}} \\ {d = 20\;{\text{mm}}} \end{array}} \right. $$ 在Matlab Robotic Toolbox中建立机器人模型进行仿真,结果如图16所示。
图16所示为两个机器人的初始位置,$ {i_1} $在左侧,基坐标系与世界坐标系一致,$ {i_2} $在右侧,基坐标系在世界坐标系中$ [1\;000,0,0] $。写字板的轨迹如图17所示。
写字板作直线运动,从$ [500,500,600] $到$ [500, - 500,600] $,运动过程中,$ {i_1} $各关节的角位移变化如图18所示。
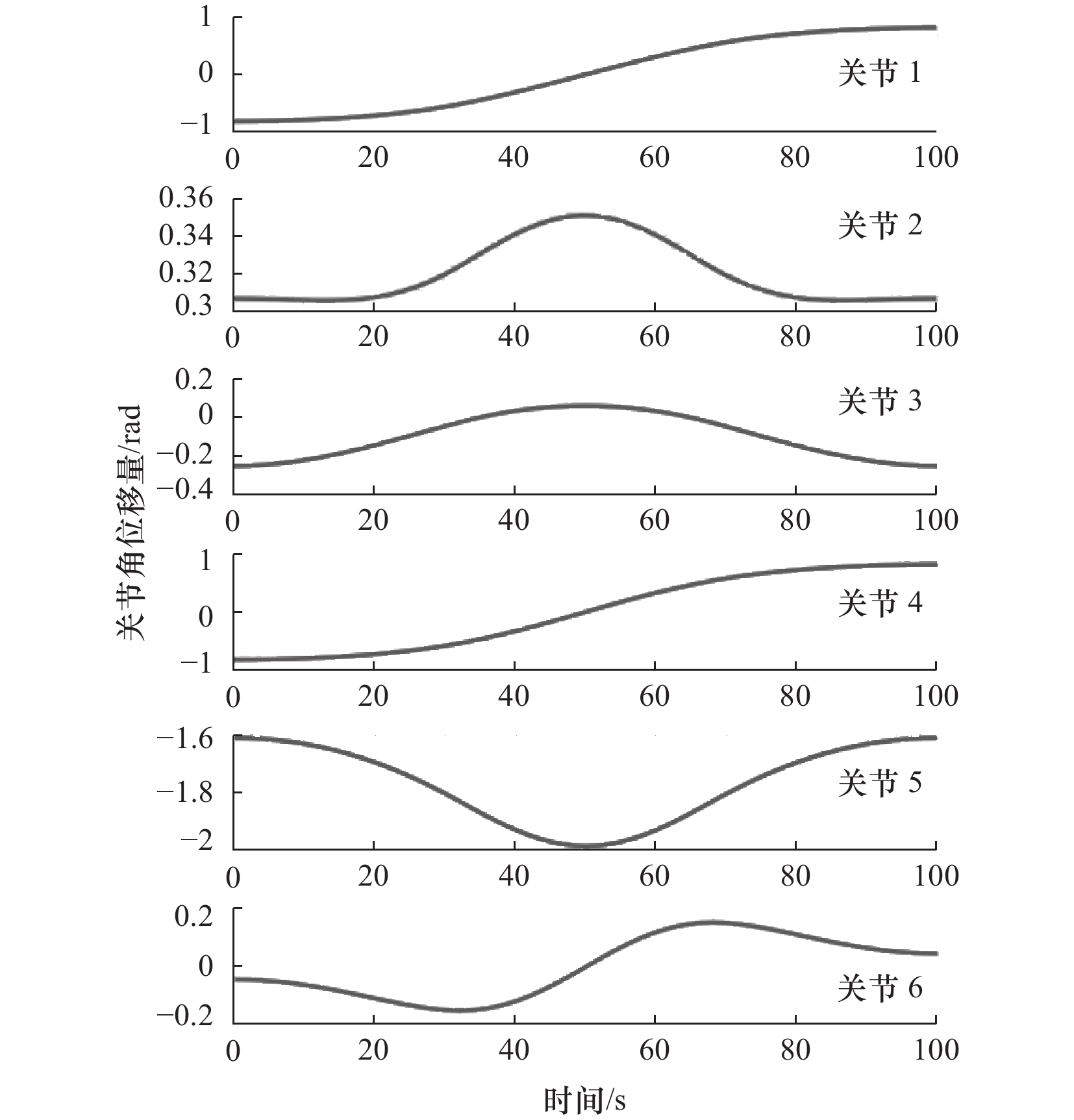
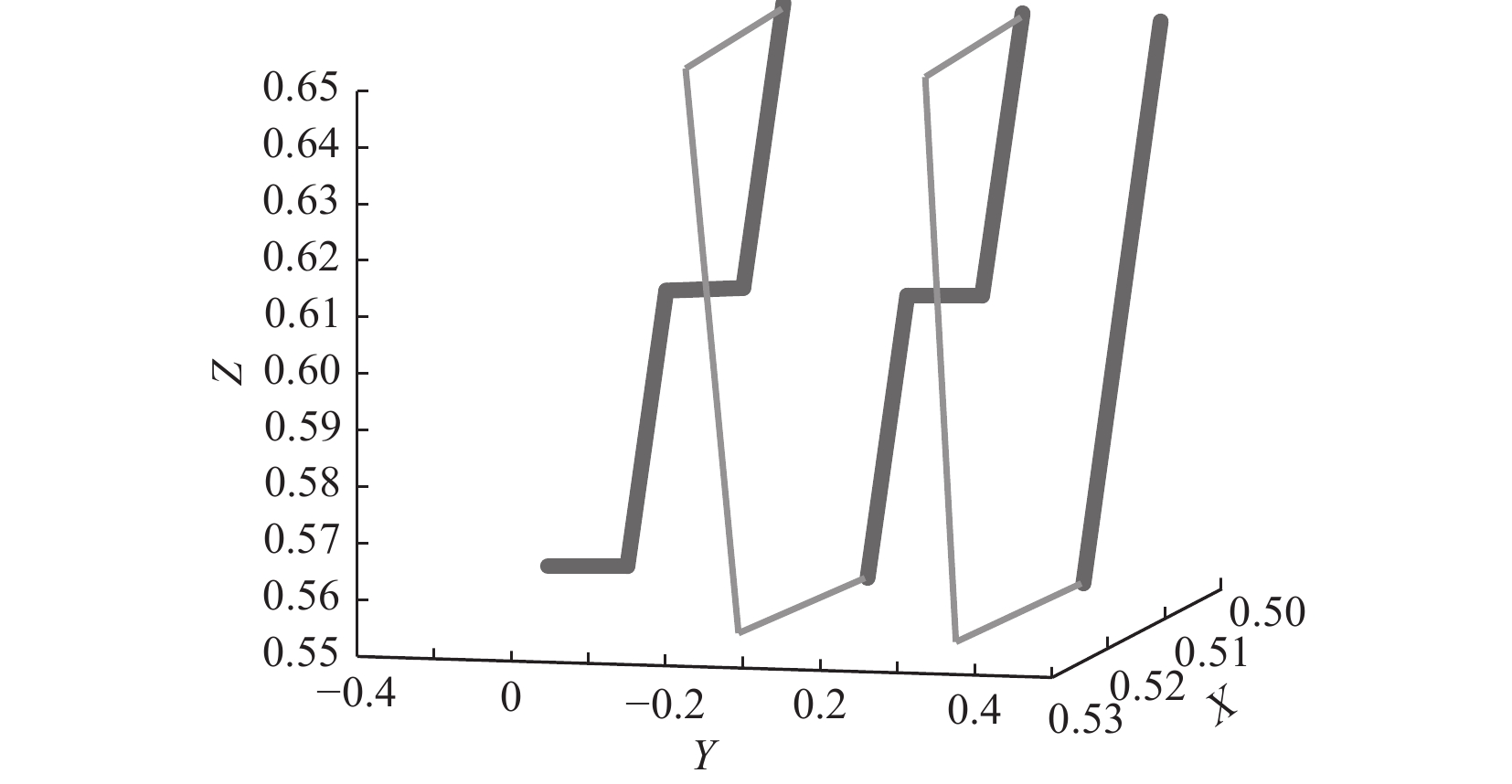
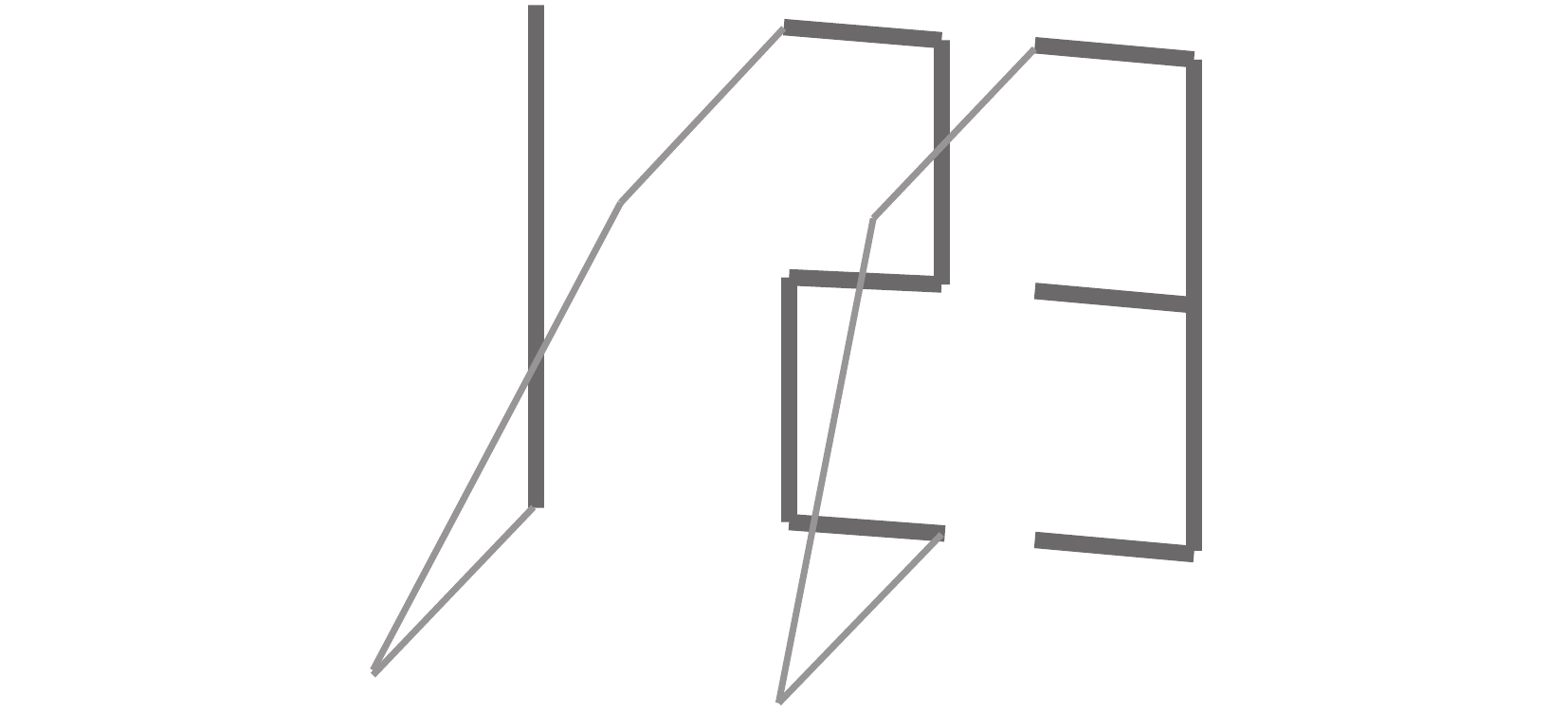
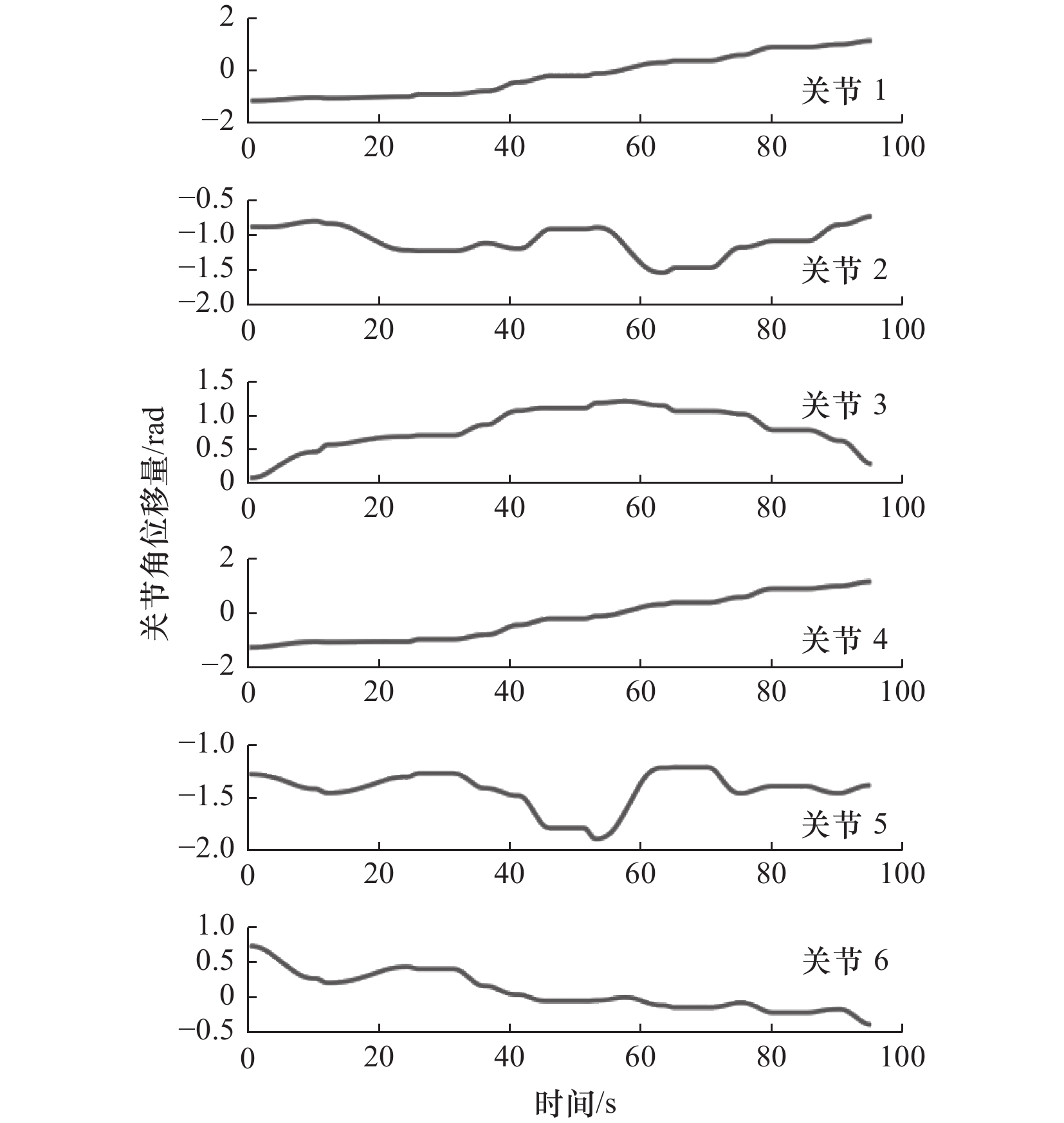
从图中可以看到,主机器人写字板是直线运动,各关节角的变化较小。$ {i_2} $工具坐标系原点在笔尖,仿真结果如图19所示。当$ {i_1} $运动时,写字笔会写下任务要求的文字,运动轨迹如图20所示。粗线是书写轨迹,细线是起笔、落笔、移动的轨迹,写字笔沿着世界坐标系$ y $轴正向移动。“2”和“3”中缺少的“—”,可由写字板沿着$ y $轴正方向移动写出对。写出的标准字迹如图21所示,能够看到,书写过程非常顺畅,每一次抬笔落笔都能精确地移动到相应位置,$ {i_2} $的各个关节的角位移如图22所示。
由图18可知,$ {i_1} $各关节角位移光滑平坦,这是由于$ {i_1} $的运动只有$ y $轴上的平移,不需要关节角发生快速改变。由图22可知,$ {i_2} $各关节角的变化比较复杂,这是因为为了书写所需的笔迹,机器人需要在空间中频繁移动,但曲线上整体没有突出拐点,关节的变化相对平稳。两机器人的运动都是可以实现的,在运动过程中每个关节的变形都是平缓的。通过以上实验,证明了该方法的正确性及有效性。
5. 结语
双机器人之间的协同运动,最重要的就是它们的轨迹是否符合任务要求。本文的研究内容分为紧约束搬运任务和松约束书写任务,对运动轨迹规划的理论方法进行了分析设计,用 Matlab测试了两种方法的正确性及稳定性。实验证明,两台机械臂均能很好地完成提前设定的任务,并且各关节角位移变化平缓、没有突兀的拐点,这对于研究两台机械臂的协同控制有一定的理论价值。
-
表 1 D-H 参数表
关节 $ {\theta _i} $ $ {d_i} $ $ {a_{i - 1}} $ $ {\alpha _{i - 1}} $ 1 (−170°,170°) 387 0 0 2 (−95°,135°) 0 25 −90° 3 (−195°,70°) 0 321 0 4 (−180°,180°) 293 32 −90° 5 (−105°,105°) 0 0 90° 6 (−360°,360°) 112 0 −90° -
[1] Saridis G N. Intelligent robotic control[J]. IEEE Transactions on Automatic Control,2016,28(5):547-557.
[2] Kasagami F ,Ishimatsu T ,Watanabe S ,et al. Coordinated motion of arc welding robots using parallel data processor [C]. Industrial Electronics,Control,Instrumentation,and Automation,1992(2):656-663.
[3] 李洋,徐达,周诚. 双机器人的协同路径规划[J]. 农业机械学报,2019,50(3):358-367. DOI: 10.6041/j.issn.1000-1298.2019.03.041 [4] 王雷. 双机器人主从协调控制系统研究[J]. 工业控制计算机,2017,30(5):55-57. DOI: 10.3969/j.issn.1001-182X.2017.05.024 [5] 孟石,戴先中,甘亚辉. 多机器人协作系统轨迹约束关系分析及示教方法[J]. 机器人,2012(5):546-552. [6] 陈钢,孙丰磊,李彤,等. 考虑弹性变形的月面表取机械臂精度补偿方法[J]. 南京航空航天大学学报,2021,53(1):1-10. DOI: 10.16356/j.1005-2615.2021.01.001 [7] Howell T,Jackson B,Manchester Z. Altro:a fast solver for constrained trajectory optimization [C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS),2019:7674-7679.
[8] 张振宇,钟佩思,王祥文,等. 双工业机器人不同约束下协同运动轨迹规划[J]. 制造技术与机床,2023(6):26-32. [9] Dai J,Zhang Y,Deng H. Bidirectional RRT*-based path planning for tight coordination of dual redundant manipulators[J]. Machines,2023,11(2):209. DOI: 10.3390/machines11020209
[10] 胡宇航,张尚盈,张晓艳. 基于MATLAB的6R机械臂运动学的仿真研究[J]. 制造技术与机床,2022(11):27-32.



 下载:
下载: